>	restart:#"m11_p40"

Se tiene un depósito esférico de aluminio de 5 mm de espesor y 0,5 m de diámetro interior lleno de oxígeno líquido a 1 MPa. El depósito está aislado por una capa de 0,2 m de lana de vidrio, recubierto por una lámina de plástico de 3 mm de espesor y 0,2 W/(m×K) de conductividad, estimándose los coeficientes de convección en el líquido y en el aire ambiente en 200 W/(m2×K) y 10 W/(m2×K), respectivamente. Se pide:
a) Hacer un esquema del perfil de temperatura esperado en régimen estacionario, y estimar el orden de magnitud del calor transmitido (suponiendo paredes de pequeño espesor, geometría plana, etc.).
b) Para un elemento diferencial radial genérico de aislante, plantear el balance energético no estacionario de la cáscara esférica, e integrar para el caso estacionario.
c) Calcular la cantidad de oxígeno que habría que evacuar para mantener la presión.   

Datos:

>	read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):

>	su1:="O2":su2:="Aluminio_anodizado":su3:="Vidrio_(lana)":dat:=[LAlu=0.005*m_,D=0.5*m_,p1=1e6*Pa_,LAis=0.2*m_,LPla=0.003*m_,kPla=0.2*W_/(m_*K_),hoxi=200*W_/(m_^2*K_),hair=10*W_/(m_^2*K_)];

Eqs. const.:

>	gdat:=get_gas_data(su1):ldat:=get_liq_data(su1):Aludat:=get_sol_data(su2):Aisdat:=get_sol_data(su3):get_pv_data(su1):dat:=op(dat),gdat,ldat,Const,SI2,SI1:

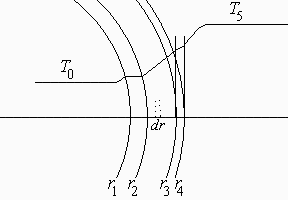
a) Hacer un esquema del perfil de temperatura esperado en régimen estacionario, y estimar el orden de magnitud del calor transmitido (suponiendo paredes de pequeño espesor, geometría plana, etc.).

Cuidado, T0=T(r=0)=Tv_oxi, T5=288 K.

Tomemos un área media, Am=(Amin+Amax)/2.

>

Qdot:=U*Am*(T5-T0);T5_:=subs(dat,T0);T0_:=subs(dat,evalf(subs(dat,solve(p1=pv(T),T))));Amin:=Pi*D^2;Amin_:=evalf(subs(dat,Amin));Amax:=4*Pi*(D/2+LAlu+LAis+LPla)^2;Amax_:=evalf(subs(dat,Amax)):'Amax'=evalf(%,2);Am:='(Amin+Amax)/2';Am_:=(Amin_+Amax_)/2;U:=1/(1/hoxi+LAlu/kAlu+LAis/kAis+LPla/kPla+1/hair);U_:=subs(dat,kAlu=k,Aludat,kAis=k,Aisdat,dat,U);U:=1/(LAis/kAis);U_:=subs(dat,kAis=k,Aisdat,dat,U);Qdot_:=subs(dat,U_*Am_*(T5_-T0_));Qdot_min_:=subs(dat,U_*Amin_*(T5_-T0_));Qdot_max:=subs(dat,U_*Amax_*(T5_-T0_));

b) Para un elemento diferencial radial genérico de aislante, plantear el balance energético no estacionario de la cáscara esférica, e integrar para el caso estacionario.

>	eqBE:=rho*4*Pi*r^2*dr*c*diff(T(r,t),t)=k*4*Pi*(r+dr)^2*(diff(T(r,t),r)+diff(T(r,t),r,r)*dr)-k*4*Pi*r^2*diff(T(r,t),r)+4*Pi*r^2*dr*phi;subs(dr=0,expand(%/(rho*4*Pi*r^2*dr*c)));

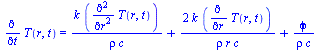Integración para el caso estacionario y sin fuentes:

>	Qdot:='Qdot':eqBE_:=0=a*diff(T(r),r,r)+2*a*diff(T(r),r)/r;dsolve(eqBE_,T(r));assign(%);sol2_:=solve({subs(r=ri,T(r))=Ti,subs(r=re,T(r))=Te,Qdot=-k*4*Pi*ri^2*subs(r=ri,diff(T(r),r))},{_C1,_C2,Qdot});

i.e. la resistencia térmica de una cáscara esférica es R=Q/DT=(re-ri)/(4*Pi*ri*re*k).

c) Calcular la cantidad de oxígeno que habría que evacuar para mantener la presión.

>

mdot:=Qdot/hlv1;Qdot:=(T5-T0)/Rtotal;Qdot:=(T5-T0)/(1/(hoxi*Pi*D^2)+LAlu/(4*Pi*D/2*(D/2+LAlu)*kAlu)+LAis/(4*Pi*(D/2+LAlu)*(D/2+LAlu+LAis)*kAis)+LPla/(4*Pi*(D/2+LAlu+LAis)*(D/2+LAlu+LAis+LPla)*kPla)+1/(hair*4*Pi*(D/2+LAlu+LAis+LPla)^2));Qdot_:=subs(dat,evalf(subs(T0=T0_,T5=T5_,dat,kAlu=k,Aludat,kAis=k,Aisdat,dat,Qdot))):'Qdot'=evalf(%,3);hlv1_:=subs(dat,T=T0_,dat,hlv(T));mdot_:=evalf(subs(dat,Qdot_/hlv1_),2);

i.e. el flujo de calor total (potencia térmica) recibido es de 46 W (no era muy mala la aproximación plana de 55 W), lo que causa una vaporización de 0,24 g/s que habrá que evacuar para que no aumente la presión.

>