>	restart:#"m11_p38"

En un catlogo se dice que haciendo circular agua a 80 C por un tubo de cobre de 28 mm de dimetro con aletas de aluminio de 1 mm de espesor cuya dimetro exterior es de 88 mm, coaxiales y espaciadas uniformemente 9 mm, se consigue transferir ms de 500 W por metro de 'radiador' al aire ambiente (se trata de la calefaccin de un autobs con el agua caliente del motor, y se tomar 20 C para la temperatura del aire y 10 W/(m2.K) de coeficiente de conveccin natural). Se pide:

a) Hacer un esquema del radiador y calcular la potencia trmica si no hubiera aletas.

b) Para no tener que resolver el problema de la aleta circular, considrese el problema de una aleta plana de longitud la de la circunferencia interior y calclese el calor que fluira por la raiz de la aleta.

c) Para no tener que resolver el problema de la aleta circular, considrese el problema del disco isotermo y calclese el calor que fluira por la raiz de esa aleta 'superconductora'.

d) Resolver el problema de una aleta circular analticamente.

e) Resolver numricamente la aleta circular y calcular la potencia trmica por metro de radiador.

Datos:

>	read`../therm_eq11.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):

>	su:="Aluminio_anodizado":dat:=[R=14e-3*m_,Q/L=500*W_/m_,L=1*m_,Tb=(80+273)*K_,Ta=(20+273)*K_,h=10*W_/(m_^2*K_),e=1e-3*m_,DR=30e-3*m_,De=9e-3*m_];

Eqs. const.:

>	sdat:=get_sol_data(su):dat:=op(dat),sdat,Const,SI2,SI1:

a) Hacer un esquema del radiador y calcular la potencia térmica si no hubiera aletas.

>	Q_L:=h*2*Pi*R*(Tb-Ta);Q_L_:=subs(dat,evalf(subs(dat,Q_L*m_)))/m_;

i.e. las aletas son fundamentales (hacen pasar de 53 W/m a 500 W/m.

b) Para no tener que resolver el problema de la aleta circular, considrese el problema de una aleta plana de longitud la de la circunferencia interior y calclese el calor que fluira por la raiz de la aleta.

>	eq11_12;eqm:=eq11_13;eq11_14;eq11_15;eq11_16;eqm_:=evalf(subs(p=2*2*Pi*R,A=2*Pi*R*e,dat,eqm));Q_1_fin:=m*k*A*(Tb-Ta)*tanh(sqrt(m*DR));Q_1_fin_:=evalf(subs(eqm_,A=e*2*Pi*R,dat,SI0,Q_1_fin))*W_;

i.e. 5,3 W por aleta.

c) Para no tener que resolver el problema de la aleta circular, considrese el problema del disco isotermo y calclese el calor que fluira por la raiz de esa aleta 'superconductora'.

>	eq_1_fin:='Q_1_fin'=h*(2*Pi*((R+DR)^2-R^2))*(Tb-Ta);Q_1_fin_:=subs(dat,evalf(subs(dat,h*(2*Pi*((R+DR)^2-R^2))*(Tb-Ta))));

>

i.e. saldrían 6,6 W por aleta si fuese isoterma (k enorme).

d) Resolver el problema de una aleta circular analticamente.

>	eqm;eqp:=p=2*2*Pi*r;eqA:=A=2*Pi*r*e;eqm_:=evalf(subs(eqp,eqA,dat,eqm));eqBE:=0=-k*A*Diff(T,r,r)-k*Diff(A,r)*Diff(T,r)+h*p*(T[inf]-T);eqBE:=diff(T(r),r,r)+diff(A(r),r)*diff(T(r),r)/A(r)=m^2*(T(r)-Tinf);dsol1:=dsolve({subs(A(r)=2*Pi*r*e,Tinf=Ta,eqBE),T(R)=Tb,D(T)(R+DR)=0},T(r));

e) Resolver numricamente la aleta circular y calcular la potencia trmica por metro de radiador.

>

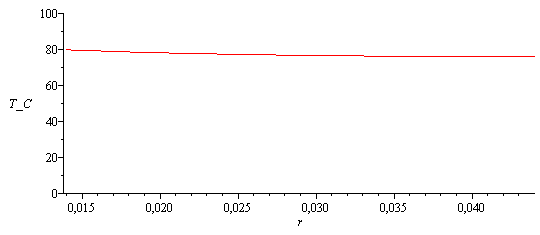
Ttip_:=evalf(subs(dsol1,eqm_,r=R+DR,dat,SI0,T(r)))*K_;'Ttip'=TKC(Ttip_);plot(subs(dsol1,eqm_,dat,SI0,T(r)-T[tr]),r=subs(dat,SI0,R)..subs(dat,SI0,R+DR),T_C=0..100);Q_1_fin:=-k*2*Pi*R*e*diff(T(r),r);n_fin_L:=L/(e+De);n_fin_L_:=round(subs(dat,%));Q_L:=h*2*Pi*R*(L-'e*n_fin_L')*(Tb-Ta)+'Q_1_fin'*'n_fin_L';

>	Q_1_fin_:=evalf(subs(r=R,dat,SI0,eval(subs(dsol1,eqm_,-k*2*Pi*R*e*diff(T(r),r)))))*W_;'Q_1_fin*n_fin_L'=evalf(Q_1_fin_*n_fin_L_);Q_L_no_fin_:=subs(dat,evalf(subs(dat,h*2*Pi*R*(L-e*n_fin_L_)*(Tb-Ta))));Q_L_:=%+rhs(%%);

Las aproximaciones previas no eran malas.

Las aletas son fundamentales. El efecto térmico del espesor de la aleta es despreciable (lo que importa es el área bañada) y se elige por rigidez.

La separacin entre aletas parece que convendría reducirse al máximo, pero ello, y el resto de la geometría, influye en el coeficiente de convección que aquí se ha supuesto constante.

>