>	restart:#"m11_p37"

En un cierto instante, t0, el perfil de temperaturas unidimensional, en una pared plana de un material de propiedades constantes, viene dado por una función T(x). Se pide:

a) Establecer la ecuación de la transmisión de calor sin fuentes ni sumideros de energía e indicar qué restricciones impone sobre la función T(x).

b) Establecer la ecuación de la transmisión de calor con fuentes y sumideros de energía e indicar qué restricciones impone sobre la función T(x) en el estado estacionario.
c) ¿Qué tipo de perfil de temperatura se daría si en la pared tuviera lugar una reacción química que liberase energía térmica en cantidad proporcional a la temperatura local? ¿Sería posible el régimen estacionario?
Datos:

>	read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):phi:='phi':

>	dat:=Const,SI1,SI2:

a) Establecer la ecuación de la transmisión de calor sin fuentes ni sumideros de energía e indicar qué restricciones impone sobre la función T(x).

>	eqHeat1:=subs(phi=0,eq11_6_11);

Cualquier d2T(x,t0)/dx2 podría compensarse con un término no-estacionario adecuado.

b) Establecer la ecuación de la transmisión de calor con fuentes y sumideros de energía e indicar qué restricciones impone sobre la función T(x) en el estado estacionario.

>	eqHeat2:=eq11_6_11;eqHeat3:=0=diff(T(x),x,x)+phi(x)/k;

La phi ha de ser la apropiada que verifique eso.

c) ¿Qué tipo de perfil de temperatura se daría si en la pared tuviera lugar una reacción química que liberase energía térmica en cantidad proporcional a la temperatura local? ¿Sería posible el régimen estacionario?

>	eqphi:=phi(x)=K*T(x);eqHeat3_:=subs(eqphi,eqHeat3);dsolve(%,T(x));

pero esa función puede presentar valores de T negativos en ciertos tramos, y la T ha de ser positiva, por lo que, o bien T(x,t0)= C*sin(x/L) está limitada a un trozo de cresta (como en la figura siguiente), o bien el régimen no es estacionario.

Un ejemplo sería:

>	Te:=400*cos(x);plot(Te,x=-1..1,Temp=0..500);eqHeat2_:=eqHeat2;eqHeat2_:=collect(diff(T(x,t),t)=a*diff(Te,x,x)+K*Te/k,cos(x));

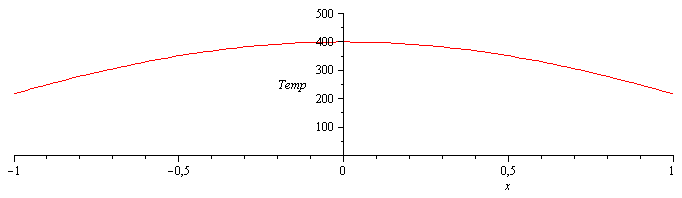que muestra que si K=k*a, el régimen es estacionario.

>