>	restart:#"m11_p36"

Considérese la difusión plana de energía térmica y de una especie química a través de un medio de espesor L, manteniendo en régimen estacionario los extremos en valores constantes. Se pide:

a) Ecuación y condiciones de contorno en cada caso.

b) Solución analítica.

c) Aplicación numérica para L=1 cm, siendo el medio aire y la especie vapor de agua evaporándose desde una superficie líquida.

Datos:

>	read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):

>	su1:="Aire":su2:="CH3OH":su2:="H2O":dat:=[L=0.01*m_];

Eqs. const.:

>	Adat:=get_gas_data(su1):Adat:=op(subs(M=M[a],[Adat]));Ygdat:=get_gas_data(su2):Yldat:=get_liq_data(su2):Ydat:=op(subs(M=M[v],[Ygdat,Yldat])):get_pv_data(su2):dat:=op(dat),Adat,Const,SI1,SI2:

a) Ecuación y condiciones de contorno en cada caso.

Eqs. balance:

>	eqBM:=diff(rho(x,t),t)=-'diff(rho(x,t)*v(x,t),x)';eqBM_:=v(x,t)=V;eqBMi:='diff(rhoi(x,t),t)=Di*diff(rhoi(x,t),x,x)-diff(rhoi(x,t)*v(x,t),x)';eqBMi_:=0=Di*diff(yi(x),x,x)-diff(yi(x)*V,x);eqBE:=subs(phi=0,eq11_6_11);eqBE_:=0=a*diff(T(x),x,x);

b) Solución analítica.

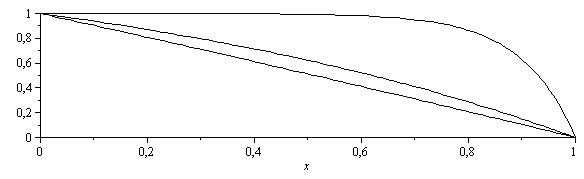
Nótese que el balance energético da una recta pero el másico sólo la da si V<<Di/L.

>

eqBC1:=T(0)=T0;eqBC2:=T(L)=T1;dsolT:=dsolve({eqBE_,eqBC1,eqBC2},T(x));eqBC1:=yi(0)=yi0;eqBC2:=yi(L)=yi1;dsolyi:=dsolve({eqBMi_,eqBC1,eqBC2},yi(x));dsolyilin:=yi(x)=collect(simplify(convert(series(rhs(dsolyi),V=0,3),polynom)),x);plot([seq(subs(yi1=0,yi0=1,L=1,V=1,Di=10^i,rhs(dsolyi)),i=-1..1)],x=0..1,color=black);

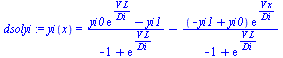Pero la V se obtiene de la ecuación de Fick:

>	eqFick:=rho*V=eval(-rho*Di*subs(x=0,diff(subs(dsolyi,yi(x)),x)));eqFick:=rho*V=convert(series(rhs(%),V=0,2),polynom);

y V<<Di/L sólo si yi<<1.

c) Aplicación numérica para L=1 cm, siendo el medio aire y la especie vapor de agua evaporándose desde una superficie líquida.

>	eqBC0:=yi0=x[v]*M[v]/(x[v]*M[v]+x[a]*M[a]);eqBC0:=yi0=x[v]*M[v]/M[a];eqBC0:=yi0='(M[v]/M[a])*pv(T)/p0';eqBC0_:=evalf(subs(T=T0,dat,Ydat,dat,eqBC0));

Suponiendo una humedad ambiente del 50%:

>	eqBC1:=yi1=yi0*phi;eqBC1_:=subs(phi=0.5,eqBC0_,yi1=yi0*phi);

Para el aire, tomando Di=a=k/(rho*cp):

>	eqD:=a=k/(rho*c[p]);eqD:=a=k*R*T0/(p0*c[p]);eqD_:=subs(dat,eqD);eqD__:=subs(dat,nu=mu*R*T0/p0);eqD:=Di=a;V_:=subs(eqD,eqD_,eqBC0_,eqBC1_,dat,solve(eqFick,V));

Del balance másico en la interfase líquida:

>	eqBM0:=-(p0/(R*T0))*Di*(yi1-yi0)/L=-rholiq*dx0/dt;eqBM0_:=dx0_dt_=solve(subs(eqD,eqD_,rholiq=rho,Ydat,eqBC0_,eqBC1_,dat,eqBM0),dx0)/dt;'dx0_dt_'=rhs(%)*(86400*s_/dia_)*(1000*mm_/m_);

es decir, se evapora menos de 1 mm/dia (sólo válido sin convección, p.e. en un tubo de ensayo).

Para la difusión térmica pura, sin difusión de masa, sería:

>	eqFourier:=-k*(T1-T0)/L;

que para 1 cm de aire, por unidad de área y de salto térmico sería:

>	eqFourier_:=subs(T1=1*K_+T0,dat,SI1,eqFourier)/K_;

Pero la evaporación másica lleva asociado un flujo energético, que puede provenir axialmente:

>	eqBE0:=k*(T1-T0)/L=-rholiq*(dx0/dt)*h[lv]+(p0/(R*T0))*V*c[p]*(T1-T0);eqBE0:=k*(T1-T0)/L=-rholiq*(dx0/dt)*h[lv0];DT01_:=simplify(subs(dx0=dx0_dt_*dt,eqBM0_,dat,rholiq=rho,Ydat,dat,solve(eqBE0,T1)-T0)):DT01=evalf(%,2);

Si el ambiente está a T0=15 ºC, el agua del tubo se enfriaría hasta T0-DT=7,5 ºC si las paredes del tubo fuesen aislantes; si no, el balance energético de agua sería:

>	eqBE0:=U*A[lateral]*DT+A[cross]*k*DT/L=-A[cross]*rholiq*(dx0/dt)*h[lv0];DT01__:=simplify(subs(U=5*W_/(m_^2*K_),A[lateral]=5*A[cross],dx0=dx0_dt_*dt,eqBM0_,dat,rholiq=rho,Ydat,dat,solve(eqBE0,DT))):DT01=evalf(%,2);

p.e. para U=5 W/(m2.K) y Alat/Across=5, lo que indica que normalmente la transmitancia térmica lateral es la dominante.

>