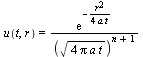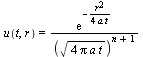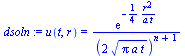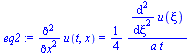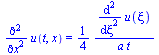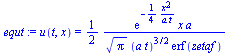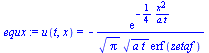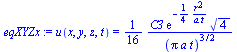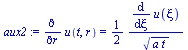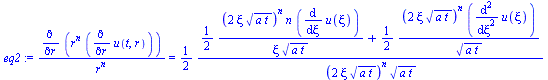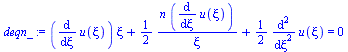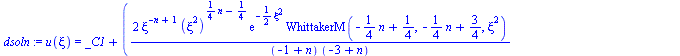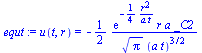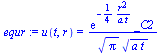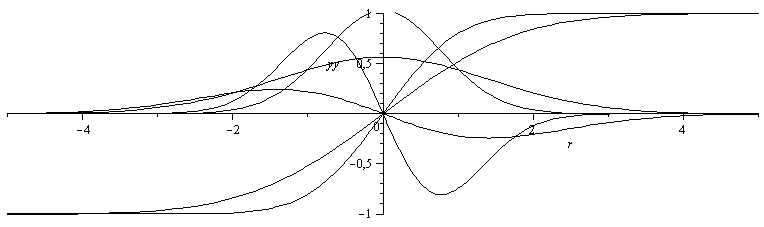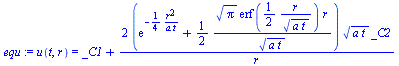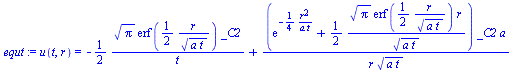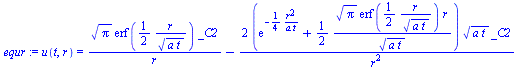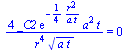>	restart:#"m11_p35"

Se trata de obtener soluciones (principales) de la ecuación del calor, du/dt=a*Laplacian(u) (es decir, sin considerar las condiciones de contorno. Se aplica a deposiciones instantáneas).

a) Demostrar que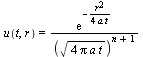

es solución para n=0=plana, n=1=cil, n=2=esf.

b) Demostrarlo mediante el cambio u/x,y,z,t)=X(x,t)Y(y,t)Z(z,t).

c) Obtener soluciones con el cambio r=xi*sqrt(4at).

Datos:

>	read`../therm_eq.m`:eq11_5_6;

Formas simétricas, i.e. unidimensionales.

Ec. general (n=0=plana, n=1=cil, n=2=esf):

>	deq:=diff(u(t,r),t)-a*(1/r^n)*'diff(r^n*diff(u(t,r),r),r)'=0;

Solución particular general (n=0=plana, n=1=cil, n=2=esf):

>	dsoln:=u(t,r)=exp(-r^2/(4*a*t))/sqrt(4*Pi*a*t)^(n+1);

Comprobación:

>	for n from 0 to 2 do expand(deq);simplify(expand(eval(subs(dsoln,deq))));od;n:='n':

a) Obtención de soluciones por separación de variables:

>	eqSepVar:=u(x,y,z,t)=X(x,t)*Y(y,t)*Z(z,t);with(linalg):deq0:=diff(u(x,y,z,t),t)-a*laplacian(u(x,y,z,t),[x,y,z])=0;collect(expand(subs(eqSepVar,deq0)/rhs(eqSepVar)),[X,Y,Z]);

>

deqX:=subs(n=0,deq);xi(x,t):=x/sqrt(4*a*t);eq1:='diff(u(t,x),t)'=diff(u(xi),xi)*diff(xi(x,t),t);eq1_:=subs(x=xi*sqrt(4*a*t),rhs(eq1));eq2:='diff(u(t,x),x,x)'=diff(u(xi),xi,xi)*diff(xi(x,t),x)^2;subs(n=0,eq2);deqX_:=expand((-eq1_+a*rhs(eq2))*4*t=0);dsol1:=expand(dsolve(deqX_,u(xi)));equ:=u(t,x)=rhs(subs(xi=x/sqrt(4*a*t),dsol1));

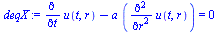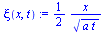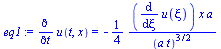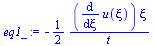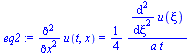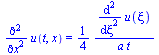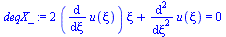Error, (in ODEtools/info) expected the indeterminate function as, say, F(x) where x is of type "name" - and also cannot be a procedure name. Received: [u(xi)]

Error, invalid input: rhs received dsol1, which is not valid for its 1st argument, expr

No funciona con la variable griega xi; cambiemos a xi_.

>	dsol1:=dsolve({2*diff(u(xi_),xi_)*xi_+diff(u(xi_),xi_,xi_)=0,u(0)=1,u(zetaf)=0},u(xi_));dsol1:=subs(xi_=xi,%);equ:=u(t,x)=rhs(subs(xi=x/sqrt(4*a*t),dsol1));

Es fácil ver que si u(t,x) es una solución de du/dt=ad2u/dx2, también lo son sus derivadas parciales de cualquier orden, luego:

>	equt:=u(t,x)=diff(rhs(equ),t);equx:=u(t,x)=diff(rhs(equ),x);

Combinando u=XYZ queda:

>	eqXYZ:=u(x,y,z,t)=subs(_C1=0,rhs(equ)*subs(x=y,rhs(equ))*subs(x=z,rhs(equ)));eqXYZ:=u(x,y,z,t)=C2*erf(r/sqrt(4*a*t));eqXYZt:=u(x,y,z,t)=subs(_C1=0,rhs(equt)*subs(x=y,rhs(equt))*subs(x=z,rhs(equt)));eqXYZx:=u(x,y,z,t)='C3*exp(-r^2/(4*a*t))/(4*Pi*a*t)^(3/2)';

Esta última coincide con dsoln para x2=r2, para x2+y2=r2, y para x2+y2+z2=r2, como se quería demostrar.

b) Obtención de soluciones por otro camino:

>

xi(r,t):=r/sqrt(4*a*t);eq1:='diff(u(t,r),t)'=diff(u(xi),xi)*diff(xi(r,t),t);eq1_:=subs(r=xi*sqrt(4*a*t),rhs(eq1));aux1:='(r^n)'=(xi*sqrt(4*a*t))^n;aux2:='diff(u(t,r),r)'=diff(u(xi),xi)*diff(xi(r,t),r);eq2:='(1/r^n)*diff(r^n*diff(u(t,r),r),r)'=(1/rhs(aux1))*diff(rhs(aux1)*rhs(aux2),xi)*diff(xi(r,t),r);

Hemos pasado de la PDE a la ODE:

>	deqn_:=expand(-2*t*(eq1_-a*rhs(eq2)=0));

cuya solución general es:

>	dsoln:=dsolve(deqn_,u(xi));dsol0:=dsolve(subs(n=0,deqn_),u(xi));dsol1:=dsolve(subs(n=1,deqn_),u(xi));dsol2:=dsolve(subs(n=2,deqn_),u(xi));

Error, (in ODEtools/info) expected the indeterminate function as, say, F(x) where x is of type "name" - and also cannot be a procedure name. Received: [u(xi)]

Error, (in ODEtools/info) expected the indeterminate function as, say, F(x) where x is of type "name" - and also cannot be a procedure name. Received: [u(xi)]

Error, (in ODEtools/info) expected the indeterminate function as, say, F(x) where x is of type "name" - and also cannot be a procedure name. Received: [u(xi)]

Error, (in ODEtools/info) expected the indeterminate function as, say, F(x) where x is of type "name" - and also cannot be a procedure name. Received: [u(xi)]

Otra vez cambiamos xi a xi_.

>	dsoln:=subs(xi_=xi,dsolve(subs(xi=xi_,deqn_),u(xi_)));dsol0:=subs(xi_=xi,dsolve(subs(n=0,xi=xi_,deqn_),u(xi_)));dsol1:=subs(xi_=xi,dsolve(subs(n=1,xi=xi_,deqn_),u(xi_)));dsol2:=subs(xi_=xi,dsolve(subs(n=2,xi=xi_,deqn_),u(xi_)));

La solución plana (n=0) da la función error (y sus derivadas)

>	equ:=u(t,r)=rhs(subs(xi=r/sqrt(4*a*t),dsol0));simplify(eval(subs(equ,n=0,deq)));equt:=u(t,r)=diff(rhs(equ),t);simplify(eval(subs(equt,n=0,deq)));equr:=u(t,r)=diff(rhs(equ),r);simplify(eval(subs(equr,n=0,deq)));

>	plot({op(subs(_C1=0,_C2=1,a=1,t=1,{rhs(equ),rhs(equt),rhs(equr)})),op(subs(_C1=0,_C2=1,a=1,t=0.3,{rhs(equ),rhs(equt),rhs(equr)}))},r=-5..5,yy=-1..1,color=black);

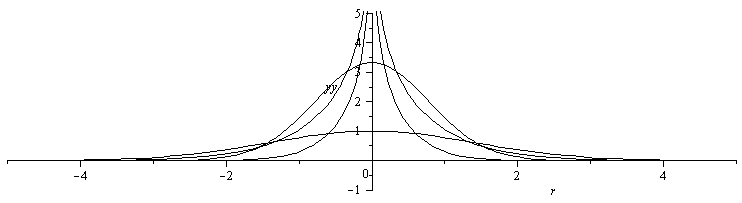
La solución cilíndrica (n=1) da la función Integral-exponencial (y su derivada temporal, ya que la derivada espacial no es solución)

>	equ:=u(t,r)=rhs(subs(xi=r/sqrt(4*a*t),dsol1));simplify(eval(subs(equ,n=1,deq)));equt:=u(t,r)=diff(rhs(equ),t);simplify(eval(subs(equt,n=1,deq)));equr:=u(t,r)=diff(rhs(equ),r);simplify(eval(subs(equr,n=1,deq)));

>	plot({op(subs(_C1=0,_C2=1,a=1,t=1,{rhs(equ),rhs(equt)})),op(subs(_C1=0,_C2=1,a=1,t=0.3,{rhs(equ),rhs(equt)}))},r=-5..5,yy=-1..5,color=black);

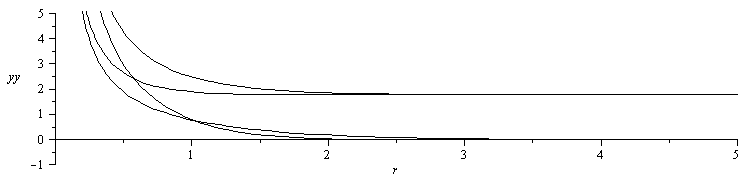
La solución esférica (n=2) da la función Integral-exponencial (y su derivada temporal, ya que la derivada espacial no es solución)

>	equ:=u(t,r)=rhs(subs(xi=r/sqrt(4*a*t),dsol2));simplify(eval(subs(equ,n=2,deq)));equt:=u(t,r)=diff(rhs(equ),t);simplify(eval(subs(equt,n=2,deq)));equr:=u(t,r)=diff(rhs(equ),r);simplify(eval(subs(equr,n=2,deq)));

>	plot({op(subs(_C1=0,_C2=1,a=1,t=1,{rhs(equ),rhs(equt)})),op(subs(_C1=0,_C2=1,a=1,t=0.3,{rhs(equ),rhs(equt)}))},r=0..5,yy=-1..5,color=black);

>