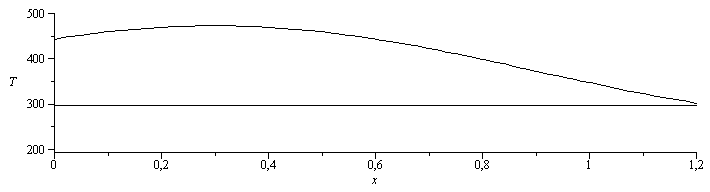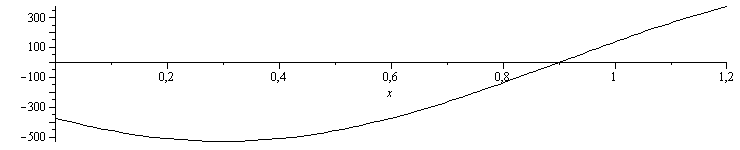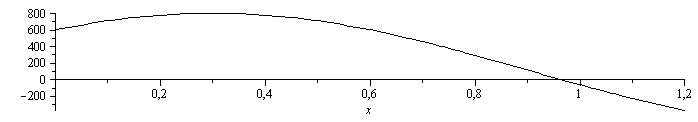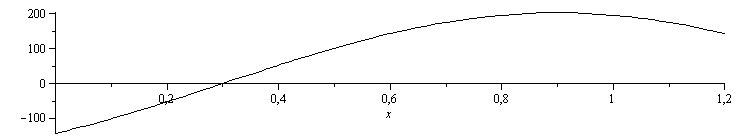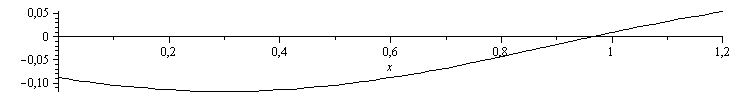>	restart:#"m11_p34"

11.34. Una varilla de cobre desnudo de 5 mm de diámetro y 1200 mm de longitud tiene una temperatura superficial expresable en función de la distancia x a un extremo por la ecuación:

cuando T se mide en K y x en mm. La varilla se encuentra rodeada de aire a 25 ºC con un coeficiente de convección que se estima en 7 W/(m2K). El régimen se supone permanente y no se considera la influencia de la radiación. Se pide:
a) Puntos de la varilla en los que el flujo de calor transferido por conducción es máximo o mínimo.
b) Puntos de la varilla en los que el flujo de calor transferido por convección es máximo o mínimo.
c) Aporte energético a realizar a cada elemento de la varilla en función de x.

Datos:

>	read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):assume(x>0):

>	su1:="Cobre":dat:=[D=0.05*m_,L=1.2*m_,T1=(100+273)*K_,T(x)=273*K_+(T1-273*K_)*(1+sin(Pi*x/L+Pi/4)),T0=(25+273)*K_, h=10*W_/(m_^2*K_)];

>	sdat:=get_sol_data(su1):dat:=[op(dat),sdat,Const,SI1,SI2]:

a) Puntos de la varilla en los que el flujo de calor transferido por conducción es máximo o mínimo.

Primero dibujamos el perfil dado.

>	T_:=subs(dat,T(x));plot({subs(dat,SI0,T0),subs(dat,SI0,T_)},x=0..subs(dat,L/m_),'T'=200..500,color=black);Tmax_:=maximize(subs(dat,SI0,T_),x=0..subs(dat,L/m_))*K_;Tmin_:=minimize(subs(dat,SI0,T_),x=0..subs(dat,L/m_))*K_;

i.e. toda la varilla está por encima de los 298 K de la Tambiente.

Para mantener ese perfil de temperatura en régimen estacionario es necesario que existan fuentes internas.

El balance energético para un elemento, por unidad de longitud, es:

>

eq11_12;eqBEestac:=Qcondnet+Qconv+Qgen=0;Qcondnet:=k*A*diff(T(x),x,x);Qconv:=h*p*(T0-T(x));Qgen:=Phi_L;Qcondnet_:=eval(subs(dat,Qcondnet));Qcondnetmax_:=maximize(subs(A=Pi*D^2/4,p=Pi*D,dat,SI0,Qcondnet_),x=0..subs(dat,L/m_))*W_/m_;Qcondnetmin_:=minimize(subs(A=Pi*D^2/4,p=Pi*D,dat,SI0,Qcondnet_),x=0..subs(dat,L/m_))*W_/m_;plot(subs(dat,SI0,subs(A=Pi*D^2/4,dat,Qcondnet_)),x=0..subs(dat,L/m_),color=black);

b) Puntos de la varilla en los que el flujo de calor transferido por convección es máximo o mínimo.

>	'Qconv'=Qconv;Qconv_:=eval(subs(dat,Qconv));Qconvmax_:=maximize(subs(A=Pi*D^2/4,p=Pi*D,dat,SI0,Qconv_),x=0..subs(dat,L/m_))*W_/m_;Qconvmin_:=minimize(subs(A=Pi*D^2/4,p=Pi*D,dat,SI0,Qconv_),x=0..subs(dat,L/m_))*W_/m_;plot(subs(A=Pi*D^2/4,p=Pi*D,dat,SI0,Qconv_),x=0..subs(dat,L/m_),color=black);

Nótese que se corresponde con el perfil de temperatura.

c) Aporte energético a realizar a cada elemento de la varilla en función de x.

>

'0=Qgen+Qcond+Qconv';Qgen_:=simplify(-subs(A=Pi*D^2/4,p=Pi*D,dat,SI0,Qcondnet_+Qconv_));Qgenmax_:=maximize(subs(A=Pi*D^2/4,p=Pi*D,dat,SI0,Qgen_),x=0..subs(dat,L/m_))*W_/m_;Qgenmin_:=minimize(subs(A=Pi*D^2/4,p=Pi*D,dat,SI0,Qgen_),x=0..subs(dat,L/m_))*W_/m_;plot(subs(A=Pi*D^2/4,p=Pi*D,dat,SI0,Qgen_),x=0..subs(dat,L/m_),color=black);

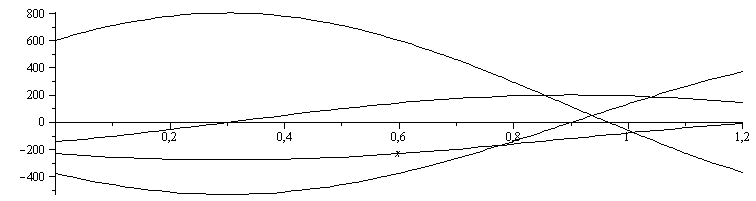
Podemos calcular también ell calor que fluye por conducción hacia la derecha en cada punto (distinto del neto antes calculado) es:

>

Qk:=-k*A*diff(T(x),x);Qk_:=simplify(subs(dat,Qk));xQknull_:=solve(Qk_=0,x);Qk0_:=subs(dat,evalf(subs(x=0,A=Pi*D^2/4,dat,Qk_)));QkL_:=subs(dat,evalf(subs(x=L,A=Pi*D^2/4,dat,Qk_)));Qkmax_:=maximize(subs(A=Pi*D^2/4,dat,SI0,Qk_),x=0..subs(dat,L/m_))*W_;Qkmin_:=minimize(subs(A=Pi*D^2/4,dat,SI0,Qk_),x=0..subs(dat,L/m_))*W_;plot(subs(dat,SI0,subs(A=Pi*D^2/4,dat,Qk_)),x=0..subs(dat,L/m_),color=black);

i.e. en x=0 salen de la varilla 140 W, y en x=L salen otros 140 W.

Si dibujamos todas las curvas juntas:

>	plot(subs(dat,SI0,subs(A=Pi*D^2/4,p=Pi*D,dat,[Qk_,Qgen_,Qconv_,Qcondnet_])),x=0..subs(dat,L/m_),color=black);

Globales:

>	Qcondglobal:='Qk0_-QkL_';Qcondglobal_:=Qk0_-QkL_;Qconvglobal_:=int(subs(p=Pi*D,dat,SI0,Qconv_),x=0..subs(dat,L/m_))*W_;Qgenglobal_:=int(subs(p=Pi*D,dat,SI0,Qgen_),x=0..subs(dat,L/m_))*W_;Qgenglobal_:=-Qcondglobal_-Qconvglobal_;

Una posible interpretación de esa distribución de fuentes es que en realidad se tratase de un estado no estacionario, y que

Qgen=rho*c*A*dT/dt:

>	dT_dt:='-Qgen_'/(rho*c*A);plot(subs(A=Pi*D^2/4,dat,SI0,dT_dt),x=0..subs(dat,L/m_),color=black);

>