>	restart:#"m11_p33"

Un tubo de acero inoxidable de diámetro interior 25 mm y 6 mm de espesor está perfectamente aislado por su exterior. El tubo transporta agua a 5 ºC respecto a la que el coeficiente de convección se estima en h=1600 W/(m2×K). El material del tubo genera energía uniformemente a razón de 2×107 W/m3. Asumiendo que el flujo de calor es exclusivamente radial y el régimen permanente, se pide:
a) Ecuación diferencial del campo de temperaturas en el tubo.
b) Detallar las condiciones de contorno aplicables.
c) Temperaturas de las caras interior y exterior del tubo.
d) Radio para el que se produce la temperatura máxima y valor de ésta.
Datos:

>	read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):

>	su1:="H2O":su2:="Acero_inox":dat:=[R1=0.0125*m_,R2=0.0185*m_,T0=(5+273)*K_,h=1600*W_/(m_^2*K_),phi=2e7*W_/m_^3];

>	dat:=op(dat),Const,SI1,SI2:Sdat:=get_sol_data(su2):Wdat:=get_liq_data(su1):

a) Ecuación diferencial del campo de temperaturas en el tubo.

>	eqBEdif:=eq11_6_20;

b) Detallar las condiciones de contorno aplicables.

>	eqBE1:=h*2*Pi*R1*(T1-T0)=k*2*Pi*R1*diff(T(r),r)[r=R1];eqBE2:=k*2*Pi*R2*diff(T(r),r)[r=R2]=0;

c) Temperaturas de las caras interior y exterior del tubo.

Podemos hacer primero un balance energético global del tubo (todo lo que se genera va al agua):

>	eqBE:=Pi*(R2^2-R1^2)*phi=h*2*Pi*R1*(T1-T0);T1_:=solve(%,T1);T1__:=subs(dat,%);'T1__'=TKC(%);

Y ahora integrar y obtener el perfil de temperaturas y su valor en la cara exterior del tubo.

>

eqBEdif;sol:=collect(dsolve({eqBEdif,T(R1)=T1,D(T)(R2)=0},T(r)),phi);T2_:=evalf(subs(r=R2,T1=T1__,Sdat,dat,SI0,rhs(%)))*K_;'T2_'=TKC(%);plot({[r,subs(T1=T1__,dat,Sdat,SI0,rhs(sol)),r=0.0125..0.0185],[r,subs(dat,SI0,T0+(T1__-T0)*exp(1e3*(r-R1))),r=0..0.0125],[[0.0125,0],[0.0125,1000]],[[0.0185,0],[0.0185,1000]]},r=0..0.02,T=0..500,color=black);

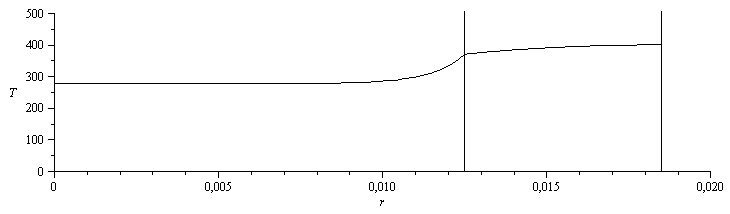En resumen, con agua a 5 ºC, la cara interna queda a 98 ºC y la exterior a 127 ºC. (La capa límite se ha simulado.)

>