>	restart:#"m11_p32"

Una varilla cilíndrica de aluminio de 5 mm de diámetro y 1 m de longitud tiene permanentemente uno de sus extremos a 450 K. Una fracción l de su longitud medida desde dicho extremo está perfectamente aislada por su exterior mediante una funda. El coeficiente convectivo con el aire ambiente, que está a 288 K, vale 15 W/(m2·K). El otro extremo de la varilla se mantiene a 350 K. Se pide, en función de l:
a) Ecuación diferencial y condiciones de contorno que determinan la distribución de temperaturas.
b) Esquematizar el perfil esperado de temperaturas de la varilla.
c) Indicar cómo se calcularía la potencia térmica total consumida para mantener el estado estacionario.
d) La temperatura del final de la funda.
Datos:

>	read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):

>	su:="Aluminio_anodizado":dat:=[R=2.5e-3*m_,L=1*m_,T1=450*K_,T0=288*K_,h=15*W_/(m_^2*K_),T2=350*K_];

Eqs. const.:

>	sdat:=get_sol_data(su):dat:=op(dat),sdat,Const,SI2,SI1:

a) Ecuación diferencial y condiciones de contorno que determinan la distribución de temperaturas.

>	eqBE:=eq11_12;eqm:=eq11_13;eqBE1:=subs(m=0,eq11_14);T1x:=dsolve(eqBE1,T(x));eqBE2:=eq11_14;T2x:=dsolve(subs(T[infinity]=T0,eqBE2),T(x));eq0:='T1x(0)'=T1;eq1:='T1x(La)=T2x(La)';eq3:='-k*A*Diff(T1x,x)[La]=-k*A*Diff(T2x,x)[La]';eq4:='T2x(L)'=T2;

b) Esquematizar el perfil esperado de temperaturas de la varilla.

(Ver arriba.)
c) Indicar cómo se calcularía la potencia térmica total consumida para mantener el estado estacionario.

Sólo se necesita potencia para mantener los extremos a esas temperaturas fijas, y el flujo de calor total sería:

>	Q=Q1+Q2;Q1:='-k*A*Diff(T1x,x)[0]';Q2:='k*A*Diff(T2x,x)[L]';

d) La temperatura del final de la funda.

Sea Ta  la temperatura al final del tramo enfundado, que dependerá de la longitud enfundada La.

>	T1x:=rhs(dsolve({eqBE1,T(0)=T1,T(La)=Ta},T(x)));T2x:=rhs(dsolve({subs(T[infinity]=T0,eqBE2),T(L)=T2,T(La)=Ta},T(x)));eq:=subs(x=La,eval(-k*A*diff(T1x,x)=-k*A*diff(T2x,x)));Ta_:=solve(%,Ta);eqm_:=evalf(subs(p=2*Pi*R,A=Pi*R^2,dat,eqm));Ta__:=evalf(subs(eqm_,dat,SI0,Ta_));plot(%,La=0..1);

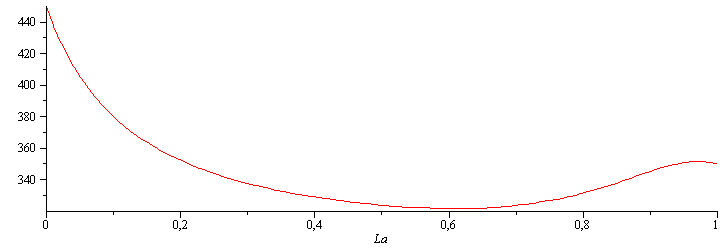¡Qué curioso!, presenta un mínimo y un máximo.

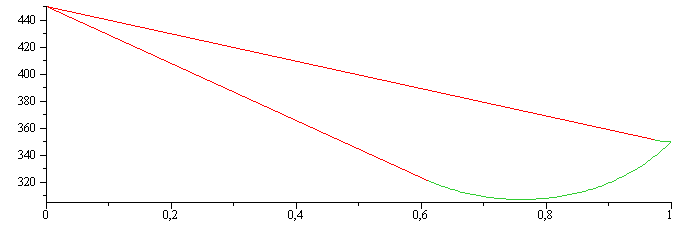
Podríamos dibujar los perfiles en estos dos casos extremos.

>	Lamin:=fsolve(diff(Ta__,La)=0,La);Lamax:=fsolve(diff(Ta__,La)=0,La=0.9..1);

>	plmin:=plot(subs(La=Lamin,eqm_,dat,SI0,{[x,subs(Ta=Ta__,T1x),x=0..Lamin],[x,subs(Ta=Ta__,T2x),x=Lamin..1]})):plmax:=plot(subs(La=Lamax,eqm_,dat,SI0,{[x,subs(Ta=Ta__,T1x),x=0..Lamax],[x,subs(Ta=Ta__,T2x),x=Lamax..1]})):with(plots):display(plmin,plmax);

>