>	restart:#"m11_p30"

Considérese un muro grueso de hormigón inicialmente a 15 ºC y que a partir de un cierto instante se mantiene una de sus caras a 250 K. Se pide:

a) Estimar el tiempo que se tardaría en bajar por debajo de 0 ºC a una profundidad de 1 cm

Datos:

>	read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):

>	su:="Hormigon":dat:=[T0=(273+15)*K_,T1=(250)*K_,T2=(273+0)*K_,L=0.01*m_];

>	sdat:=get_sol_data(su):dat:=op(dat),sdat,a=subs(sdat,k/(rho*c)),Const,SI1,SI2:

a) Estimar el tiempo que se tardaría en bajar por debajo de 0 ºC a una profundidad de 1 cm.

Si suponemos que no da tiempo a notarse el efecto del espesor finito, podemos aproximar por el modelo de sólido semi-onfinito, que admite solución de semejanza.

>

with(DEtools):eqBE:=subs(phi=0,eq11_6_11);xi(x,t):=x/sqrt(4*a*t);eq1:=lhs(eqBE)=diff(T(xi),xi)*diff(xi(x,t),t);eq2:=diff(T(x),x)=diff(T(xi),xi)*diff(xi(x,t),x);eq3:=rhs(eqBE)=a*diff(rhs(eq2),xi)*diff(xi(x,t),x);eqBE_:=subs(xi(x,t)=xi,x=xi*sqrt(4*a*t),rhs(eq1)=rhs(eq3))*4*t;dsol1:=dsolve({eqBE_,T(0)=T1,T(+infinity)=T0},T(xi));

Error, (in dsolve/func_in_args/check) the independent variable (xi in T(xi)) cannot be a procedure name

¡Vaya!, no funciona con el símbolo xi. Usando xi_:

>	dsol1:=dsolve({-2*diff(T(xi_),xi_)*xi_=diff(T(xi_),xi_,xi_),T(0)=T1,T(+infinity)=T0},T(xi_));t_:=solve(subs(dat,T2)=subs(xi_=L/sqrt(4*a*t),dat,rhs(dsol1)),t);

luego, tardará 69 s en bajar por debajo de 0 ºC a una profundidad de 1 cm

Puede estimarse el espesor mínimo para que valga este modelo, calculando a qué distancia en ese instante el salto de temperatura es todavía pequeño, e.g. DT0/10.

>	xi_L:=solve(subs(dsol1,T(xi_))=T0+(T1-T0)/10,xi_);Lm:=xi_L*sqrt(4*a*t);Lm_:=evalf(subs(t=t_,dat,%));

i.e., vale para muros con L>2 cm.

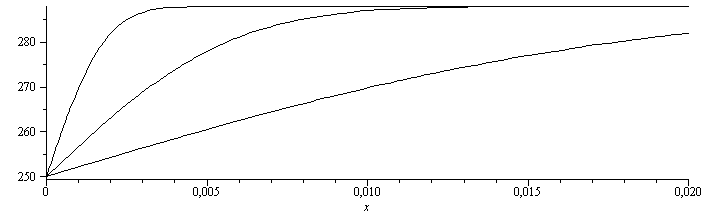
El perfil de temperaturas para t=1 s, 10 s, 100 s,... es:

>	T_:=subs(xi_=x/sqrt(4*a*t),dat,SI0,rhs(dsol1)):plot({seq(subs(t=10^i,T_),i=0..2)},x=0..0.02,color=black);

>