>	restart;#"m11_p28"

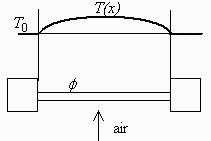
En contacto con dos bloques metálicos separados 50 cm y a temperatura ambiente de 300 K hay una varilla de aluminio de 5 mm de diámetro en cuyo interior se disipa uniformemente una potencia de 2 MW/m3, estando en régimen estacionario en presencia de una corriente de aire con la que se supone que existe un coeficiente global de convección h. Se pide:

a) Balance energético de un elemento genérico (lineal) de varilla.

b) Perfil de temperatura a lo largo de la varilla, indicando los valores extremos, suponiendo h=0.

c) Variación de entropía con el tiempo y generación de entropía para cada sistema.

d) Perfil de temperatura a lo largo de la varilla, indicando los valores extremos, suponiendo h=50   W×m-2×K-1.

Datos:

>	read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):

>	su1:="Aluminio_anodizado":dat:=[T0=300*K_,D=5e-3*m_,L=0.5*m_,phi=2e6*W_/m_^3,h=50*W_/(m_^2*K_)]:dat:=[op(dat),A=evalf(subs(dat,Pi*D^2/4))];

>	sdat:=get_sol_data(su1):dat:=op(dat),sdat,Const,SI2,SI1:

a) Balance energético de un elemento genérico (lineal) de varilla.

>	deq1:=A*(k*diff(T(x),x,x)+phi)=Pi*D*h*(T(x)-T0);deq1:=expand(deq1/(k*A));deq1:=subs(h=A*k*m^2/(Pi*D),deq1);

b) Perfil de temperatura a lo largo de la varilla, indicando los valores extremos, suponiendo h=0.

>	dsol1:=dsolve({subs(m=0,deq1),T(0)=T0,T(L)=T0},T(x));assign(%):T_:=evalf(subs(dat,T(x)));Tmax_:=subs(x=L/2,dat,T_);

i.e. el perfil será convexo, con un máximo centrado de 604 K.

c) Variación de entropía con el tiempo y generación de entropía para cada sistema.

>

dSdt:=Q/T;dSdtbloque1:=Q1/T1;Q1:=(1/2)*phi*A*L;Q1_:=subs(dat,Q1);T1:=T0;'dSdtbloque1'=evalf(subs(dat,dSdtbloque1));dSdtbloque2:=Q2/T2;dSdtbloque2:=evalf(subs(dat,dSdtbloque1));dSdtamb:=0;dSdtvarilla:=0;dSdtuniv:=subs(dat,dSdtbloque1+dSdtbloque2+dSdtamb+dSdtvarilla);Sgen:='dSdt-Q/T';Sgen_bloque1:=0;Sgen_bloque2:=0;Sgen_amb:=0;Sgen_varilla:=subs(dat,2*Q1_/T0);Sgen_univ:=Sgen_bloque1+Sgen_bloque2+Sgen_amb+Sgen_varilla;

d) Perfil de temperatura a lo largo de la varilla, indicando los valores extremos, suponiendo h=50   W×m-2×K-1.

>	T(x):='T(x)':dsol2:=dsolve(deq1):sol3:=solve({dsol1,subs(T(x)=T0,x=0,dsol1),subs(T(x)=T0,x=L,dsol1)},{_C1,_C2,T(x)}):T(x):=subs(sol3,T(x));T__:=simplify(evalf(subs(m=sqrt(Pi*D*h/(k*A)),dat,T(x))));Tmax_:=evalf(subs(x=L/2,dat,T__));plot(subs(SI0,{T_,T__}),x=0..subs(dat,L/m_),'T'=0..700,color=black);

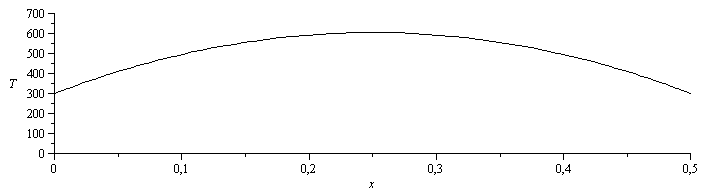i.e. el perfil es convexo con un máximo centrado de 604 K.

>