>	restart:#"m11_p26"

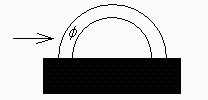
Una varilla de aluminio de 5 mm de diámetro y 30 cm de longitud, curvada en forma de semicircunferencia, tiene sus extremos apoyados en un bloque metálico muy buen conductor, que está a 100 ºC. En el interior de la varilla se disipa uniformemente una potencia de 2 MW/m3 y está en régimen estacionario en presencia de una corriente de aire ambiente con la que se supone que existe un coeficiente global de convección h=50 W/(m2K). Se pide:
a) Balance energético de un elemento genérico (lineal) de varilla.
b) Perfil de temperatura a lo largo de la varilla suponiendo h=0, indicando los valores extremos.
c) Perfil de temperatura a lo largo de la varilla, indicando los valores extremos.

Datos:

>	read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):

>	su:="Aluminio_anodizado":dat:=[R=2.5e-3*m_,L=0.3*m_,T1=(100+273)*K_,phi=2e6*W_/m_^3,h=50*W_/(m_^2*K_)];

>	sdat:=get_sol_data(su):dat:=op(dat),sdat,Const,SI2,SI1:

a) Balance energético de un elemento genérico (lineal) de varilla.

>	eqBE:=eq11_12;eq11_13;eqBE:=lhs(eq11_14)=rhs(eq11_14)-phi/k;

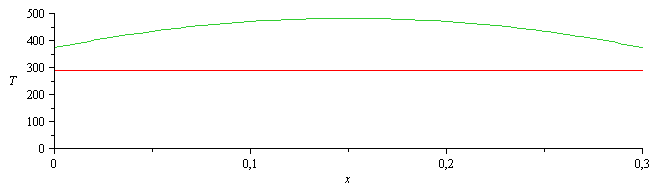
b) Perfil de temperatura a lo largo de la varilla suponiendo h=0, indicando los valores extremos.

Si h=0, entonces m=0 y queda:

>	eqBEh0:=subs(m=0,eqBE);sol1:=dsolve({eqBEh0,T(0)=T1,T(L)=T1},T(x));sol1_:=subs(dat,SI0,%);Tm:=subs(x=L/2,dat,SI0,rhs(%))*K_;plot({subs(sol1_,T(x)),subs(dat,SI0,T0)},x=0..0.3,T=0..500);

c) Perfil de temperatura a lo largo de la varilla, indicando los valores extremos.

>	sol2:=dsolve({subs(T[infinity]=T0,eq11_13,p=2*Pi*R,A=Pi*R^2,eqBE),T(0)=T1,T(L)=T1},T(x));sol2_:=evalf(subs(dat,SI0,%));Tm:=evalf(subs(x=L/2,dat,SI0,rhs(%)))*K_;plot({subs(sol2_,T(x)),subs(dat,SI0,T0)},x=0..0.3,T=0..500);

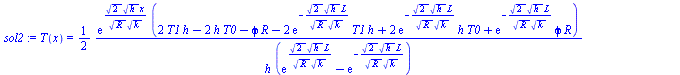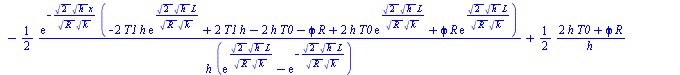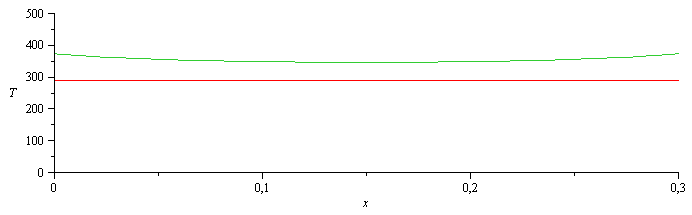Nótese que, si no hay convección, el perfil es comvexo para evacuar por los extremos toda la energía generada, mientras que si hay convección el perfil puede ser cóncavo si ésta es suficiente.

>