>	restart:#"m11_p25"

Para estimar la influencia de la profundidad de inmersión en la lectura que da un termómetro se propone el siguiente modelo. Una varilla maciza de 3 mm de diámetro, 30 cm de longitud y 1 W/(mK) de conductividad, se encuentra verticalmente sumergida una fracción a de su longitud en un líquido a 40 C con el que la transmisión de calor se supone constante y de valor h1=50 W/(m2K), estando el resto al aire, que está a 15 C y con el que la transmisión de calor se supone constante y de valor h2=5 W/(m2K). Se pide:
 1.Balance energético de un elemento diferencial lineal de varilla.
 2.Condiciones de contorno que permiten determinar el perfil de temperatura de la varilla..
 3.Temperatura en el extremo inferior en función de a.

Datos:

>	read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):assume(x>=0,a>=0,Qa<0):

>	su:="Vidrio_flint":dat:=[R=1.5e-3*m_,L=0.3*m_,k=1*W_/(m_*K_),T1=(273+40)*K_,h1=50*W_/(m_^2*K_),T0=(273+15)*K_,h0=5*W_/(m_^2*K_)];

>	sdat:=get_sol_data(su):dat:=op(dat),sdat,Const,SI2,SI1:

a)•Balance energético de un elemento diferencial lineal de varilla.

>	eqBE:=eq11_12;eq11_13;eqBE:=eq11_14;

b) Condiciones de contorno que permiten determinar el perfil de temperatura de la varilla.

Elijo el origen en la interfase. El sistema en aire va de 0 a L-a. El sistema 1 va de 0n a -a.

>

eq0:=dsolve({subs(T[infinity]=T0,m=m0,eqBE),T(0)=Ta,D(T)(L-a)=0},T(x));eq1:=dsolve({subs(T[infinity]=T1,m=m1,eqBE),T(0)=Ta,D(T)(-a)=0},T(x));qa0:=eval(subs(x=0,diff(subs(eq0,T(x)),x)));qa1:=eval(subs(x=0,diff(subs(eq1,T(x)),x)));eqTa:='qa0=qa1';eqTa:Ta_:=simplify(collect(combine(expand(solve(%,Ta)),trig),{m0,m1}));

c) Temperatura en el extremo inferior en función de a.

>

eqm0:=m0=sqrt(h0*2*Pi*R/(k*Pi*R^2));eqm1:=m1=sqrt(h1*2*Pi*R/(k*Pi*R^2));Ta__:=evalf(subs(eqm0,eqm1,dat,SI0,Ta_)):Tv0_:=evalf(subs(Ta=Ta__,eqm0,x=L-a,dat,SI0,rhs(eq0))):Tv1_:=convert(evalf(subs(Ta=Ta__,eqm1,x=-a,dat,SI0,rhs(eq1))),trig);plot({Tv0_-273,Tv1_-273,Ta__-273},a=0..subs(dat,SI0,L),TempC=0..50,axes=boxed,color=black);

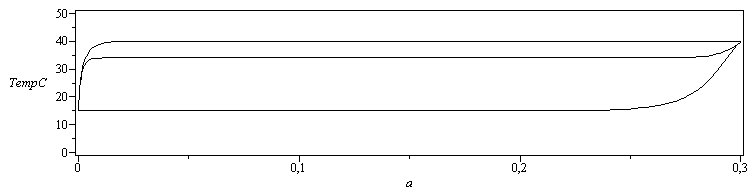i.e. esas son las temperaturas en los extremos y en la entrefase, en función de la inmersión, a.

Para a=0.1 m, el perfil de temperaturas a lo largo de la varilla es:

>	T0_:=evalf(subs(Ta=Ta__,eqm0,a=0.1,dat,SI0,rhs(eq0)));T0_L_a:=evalf(subs(x=L-a,a=0.01,dat,SI0,T0_))*K_;T1_:=evalf(subs(Ta=Ta__,eqm1,a=0.1,dat,SI0,rhs(eq1)));T0_a:=evalf(subs(x=-a,a=0.1,T1_))*K_;plot({[x,T0_-273,x=0..0.2],[x,T1_-273,x=-0.1..0]},x=-0.1..0.2,color=black);

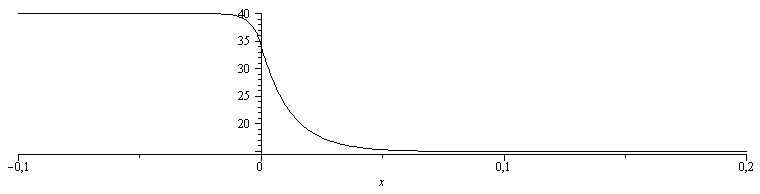donde puede verse claramente como es de suave (o brusco) el gradiente térmico al atravesar la entrefase (en muchos casos se supone un salto brusco).

>