>	restart:#"m11_p24"

Entre dos bloques metálicos a temperatura ambiente (300 K) hay una varilla de latón de 5 mm de diámetro y 50 cm de longitud en cuyo interior se disipan 2 MW/m3, estando en régimen estacionario en presencia de una corriente de aire con la que se supone que existe un coeficiente global de convección de 50 W×m-2×K-1. Se pide:

a)•Potencia total disipada.

b)•Temperatura que alcanzaría la varilla si la transmisión de calor por los extremos fuese despreciable.

c)•Balance energético de un elemento genérico (lineal) de varilla.

d)•Perfil de temperatura a lo largo de la varilla, indicando los valores extremos.

e)•Potencia transmitida al aire.

f)•Estimar la diferencia máxima de temperaturas entre el centro y la periferia de una sección transversal de la varilla.

g) Variación de entropía con el tiempo y generación de entropía para cada sistema

Datos:

>	read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):

>	su:="Laton":dat:=[T0=300*K_,R=2.5e-3*m_,L=0.5*m_,phi=2e6*W_/m_^3,h=50*W_/(m_^2*K_)];

>	sdat:=get_sol_data(su):dat:=op(dat),sdat,Const,SI2,SI1:

a)•Potencia total disipada.

>	Q:=phi*L*Pi*R^2;Q_:=subs(dat,evalf(subs(dat,Q)));

i.e. se disipan 20 W.

b) Temperatura que alcanzaría la varilla si la transmisión de calor por los extremos fuese despreciable.

>	eq1:=Q=h*A*(T-T0);Th:=solve(Q=h*2*Pi*R*L*(T-T0),T);Th_:=subs(dat,Th);'Th_'=TKC(%);

i.e. se alcanzarían 77 ºC (en el centro) con extremos aislados.

c)•Balance energético de un elemento genérico (lineal) de varilla.

>	deq1:=0=phi*Pi*R^2+k*Pi*R^2*diff(T(x),x,x)-h*2*Pi*R*(T(x)-T0);

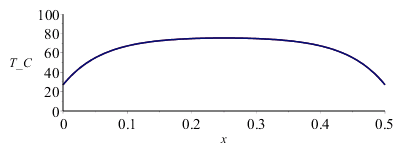
d)•Perfil de temperatura a lo largo de la varilla, indicando los valores extremos.

>	dsol1:=dsolve({deq1,T(0)=T0,T(L)=T0},T(x));dsol1_:=evalf(subs(dat,SI0,dsol1));Tmax_:=evalf(subs(x=L/2,dat,SI0,rhs(dsol1)))*K_;'Tmax_'=TKC(%);plot({rhs(dsol1_)},x=0..subs(dat,L/m_),Temp=0..400);

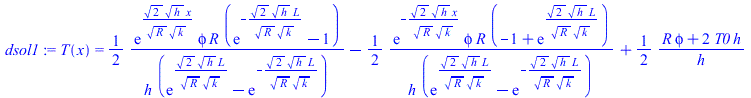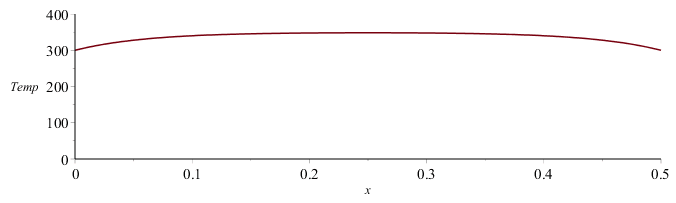i.e. solo sellegaría a 75 ºC en el centro con T0=TL=Tinf (en vez de lsos 77 ºC con extremos adiabáticos).

Puede ponerse en forma más compacta así:

>	Tcompact:=T0+(phi/(k*m^2))*(1-(sinh(m*x)+sinh(m*(L-x)))/sinh(m*L));Tcompact_:=evalf(subs(m=sqrt(2*h/(k*R)),dat,SI0,%));plot([Tcompact_-273,rhs(dsol1_)-273],x=0..0.5,T_C=0..100);

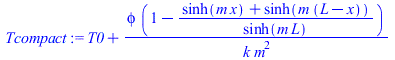e)•Potencia transmitida al aire.

>	Q1:=k*Pi*R^2*diff(T(x),x);Q1_:=simplify(subs(x=0,dat,SI0,eval(subs(dsol1,Q1))))*W_;Qaire:='Q-2*Q1';Qaire_:=Q_-2*Q1_;

i.e. se transmiten 15 W al aire y 2,4 W a cada bloque.

f)•Estimar la diferencia máxima de temperaturas entre el centro y la periferia de una sección transversal de la varilla.

>	eq11_6_20;dsol2:=dsolve({eq11_6_20,D(T)(0)=0,T(R)=TR},T(r));DT:=expand(subs(r=0,rhs(%))-TR);DT_:=subs(dat,%);

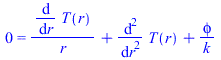i.e. despreciable, como era de prever.

g) Variación de entropía con el tiempo y generación de entropía para cada sistema

>	DS1:='Q1/T0';DS2:='Q1/T0';DSvar:=0;DSair:='Qair/T0';Sgen1:=0;Sgen2:=0;Sgenair:=0;Sgenvar:=Qtotal/T0;Sgenvar_:=evalf(subs(dat,Q_/T0),2);

se generan 0,07 W/K.

>