>	restart:#"m11_p22"

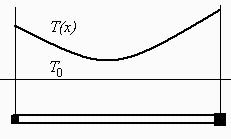
Una varilla de cobre de 4 mm de diámetro y 30 cm de longitud tiene encapsuladas en sus extremos sendas resistencias eléctricas que disipan 5 y 10 W respectivamente. Suponiendo que el coeficiente convectivo con el aire ambiente es de 10 W/(m∙K), se pide:
a) Balance energético de un elemento infinitesimal de varilla.
b) Condiciones de contorno en los extremos.
c) Perfil de temperaturas.
d) Posición de la sección de mínima temperatura.

Datos:

>	read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):assume(x>0,m>0):

>	su1:="Cobre":su2:="Hierro_fundido":dat:=[R=0.002*m_,L=0.5*m_,Q1=5*W_,Q2=10*W_,h=10*W_/(m_^2*K_)];

>	s1dat:=get_sol_data(su1):s2dat:=get_sol_data(su2):dat:=op(dat),Const,SI2,SI1:

a) .Balance energético de un elemento infinitesimal de varill

>	eq11_12;eqm:=eq11_13;eqBE:=eq11_14;

b) Condiciones de contorno en los extremos.

>	eqC1:=Q1=-k*Pi*R^2*diff(T(x),x)[x=0];eqC2:=Q2=k*Pi*R^2*diff(T(x),x)[x=L];

c)  Perfil de temperaturas.

>	dsol:=dsolve({subs(T[infinity]=Tinf,eqBE),D(T)(0)=-Q1/(k*Pi*R^2),D(T)(L)=Q2/(k*Pi*R^2)},T(x));eq11_15;

Vamos a representar gráficamente la solución para el caso de varilla de cobre y para el caso de varilla de hierro, para que se vea la diferencia.

>

eqm1_:=subs(dat,evalf(subs(p=2*Pi*R,A=Pi*R^2,dat,s1dat,eqm))):evalf(%,2);eqm2_:=subs(dat,evalf(subs(p=2*Pi*R,A=Pi*R^2,dat,s2dat,eqm))):evalf(%,2);dsol1_:=evalf(subs(Tinf=T0,eqm1_,dat,s1dat,SI0,dsol));dsol2_:=evalf(subs(Tinf=T0,eqm2_,dat,s2dat,SI0,dsol));plot(subs(dat,SI0,{[[0,T0],[L,T0]],rhs(dsol1_),rhs(dsol2_)}),x=0..subs(dat,SI0,L),Temp=0..1000,color=black);

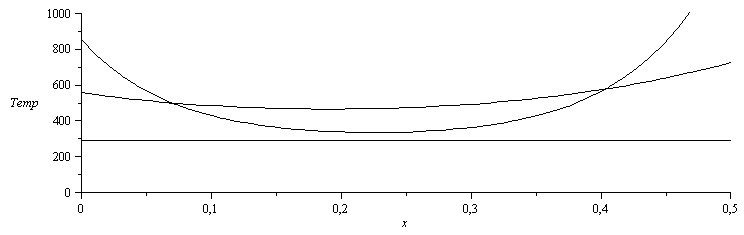Puede verse que en el caso de cobre, la varilla tiene un perfil de temperaturas más uniforme (no varía tanto).

La posición de la sección de mínima temperatura en cada caso sería:

>	xTmin1_:=solve(diff(rhs(dsol1_),x)=0,x)*m_;Tmin1_:=evalf(subs(x=xTmin1_,SI0,rhs(dsol1_)))*K_;xTmin2_:=solve(diff(rhs(dsol2_),x)=0,x)*m_;Tmin2_:=evalf(subs(x=xTmin2_,SI0,rhs(dsol2_)))*K_;

>