>	restart:#"m11_p20"

Considérese una varilla suficientemente larga de hierro de conductividad térmica 50 W/(mK) y 8 mm de diámetro en uno de cuyos extremos hay una resistencia eléctrica, de tamaño despreciable, disipando 10 W, y tómese un valor medio para el coeficiente de convección con el aire de 20 W/(m2K). Se pide:
 1.Plantear la ecuación diferencial de la transmisión de calor unidimensional a lo largo de la varilla.
 2.Especificar las condiciones de contorno apropiadas.
 3.Calcular el perfil de temperatura en la varilla.
 4.Calcular la distancia a la que la temperatura de la varilla se diferencia menos de 2 ºC de la ambiente, que es de 15 ºC

Datos:

>	read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):assume(x>0,m>0):

>	su:="Hierro_fundido":dat:=[R=0.004*m_,Q=10*W_,h=20*W_/(m_^2*K_),DT=2*K_,T0=(273+15)*K_];

>	sdat:=get_sol_data(su):dat:=op(dat),sdat,Const,SI2,SI1:

a) .Plantear la ecuación diferencial de la transmisión de calor unidimensional a lo largo de la varilla.

>	eqBE:=eq11_12;eq11_13;eqBE:=eq11_14;

b) Especificar las condiciones de contorno apropiadas.

>	eqC1:=Q=-k*Pi*R^2*diff(T(x),x)[x=0];eqC2:=0=k*Pi*R^2*diff(T(x),x)[x=+infinity];

c) Calcular el perfil de temperatura en la varilla.

>	dsol:=expand(dsolve({subs(T[infinity]=Tinf,eqBE),D(T)(0)=-Q/(k*Pi*R^2),D(T)(+infinity)=0},T(x)));

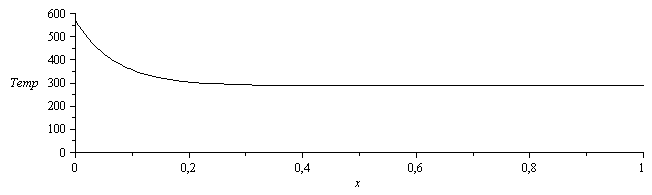
>	eqm_:=evalf(subs(p=2*Pi*R,A=Pi*R^2,dat,eq11_13));dsol1_:=evalf(subs(Tinf=T0,eqm_,dat,SI0,dsol));plot(subs(dat,SI0,{[[0,T0],[L,T0]],rhs(dsol1_)}),x=0..1,Temp=0..600,color=black);

d) Calcular la distancia a la que la temperatura de la varilla se diferencia menos de 2 ºC de la ambiente, que es de 15 ºC

>	x_:=solve(subs(T(x)=Tinf+DT,dsol),x);x__:=evalf(subs(eqm_,dat,SI0,x_),2)*m_;

i.e., a partir de unos 0,35 m la varilla ya prácticamente no transmite calor.

>