| > | restart:#"m11_p18" |
En un cilindro vertical cerrado por ambos extremos y con una válvula intermedia (célula de Loschmidt), se ha dispuesto un gas ligero en la mitad superior y uno más pesado en la mitad inferior. Determinar la evolución del perfil de concentraciones al abrir la válvula que separa ambos gases.
Datos:
| > | read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):assume(Di>0): |

Como los coeficientes de difusión mutua han de ser iguales, se trata de un problema simétrico, y, mientras no se note el efecto de los extremos, de autosemejanza.
La ecuación de la difusión, en función de la fracción másica de uno de los gases, y, será:
| > | eqFick:=diff(y(x,t),t)=Di*diff(y(x,t),x,x); |
que sólo depende de una variable combinada:
| > | eq:=eta=x/sqrt(t);eqFick:=diff(y(x/sqrt(t)),t)=Di*diff(y(x/sqrt(t)),x,x); |
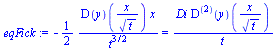 |
pasando la ecuación en derivadas parciales a la ecuación diferencial ordinaria:
| > | eqFick:=-diff(y(eta),eta)*eta=2*Di*diff(y(eta),eta,eta); |
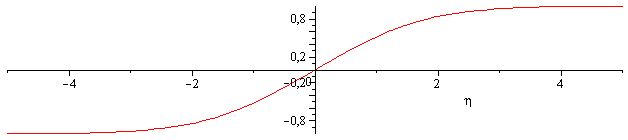
cuya solución es:
| > | sol:=dsolve({eqFick,y(0)=0,y(infinity)=1},y(eta));plot(rhs(subs(Di=1,%)),eta=-5..5); |
 |
Puede hacerse una representación dimensional con valores típicos (Di=1e-5 m2/s, L=20 cm, t=1 s, 10 s, 100 s, 1000 s:
| > | y:=erf(x/(2*sqrt(Di*t)));plot([seq(subs(Di=1e-5,t=10^i,y),i=0..3)],x=-0.1..0.1); |
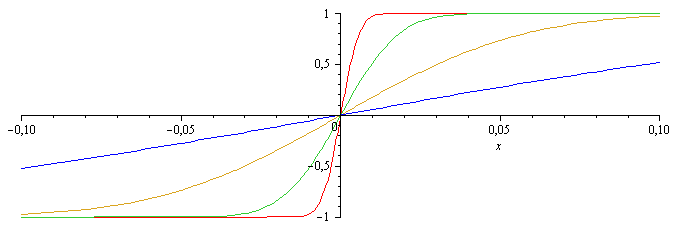 |
Nótese que en este ejemplo la difusión llega a los extremos al cabo de unos 100 s y dejaría de ser aplicable este modelo (el nuevo modelo debe dar gradiente de concentración nulo en los extremos).
| > |