>	restart:#"m11_p16"

Se trata de analizar el régimen estacionario de una instalación de agua caliente sanitaria que consta de un calentador, donde la corriente de agua recibe 20 kW, y de una tubería de 1 cm de diámetro y 10 m de longitud cuya transmitancia térmica global con el ambiente se supone que es K=200 W∙m 2∙K 1 referido al área del tubo. Se pide:
a) Temperatura de salida del calentador, T1 (en función del gasto másico de agua).
b) Perfil de temperatura a lo largo del conducto.
c) Temperatura de salida del conducto, T2, (en función del gasto másico de agua).
d) Gasto másico que daría máxima temperatura de salida del conducto y valor de ésta.
e) Comentar la viabilidad y conveniencia del punto de trabajo anterior.
Datos:

>	read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):

>	su:="H2O":dat:=[Q=20e3*W_,R=0.005*m_,L=10*m_,K=200*W_/(m_^2*K_)];

>	ldat:=get_liq_data(su):dat:=op(dat),ldat,Const,SI1,SI2:

a) Temperatura de salida del calentador, T1 (en función del gasto másico de agua).

Sea T0 la de entrada y T1 la de salida.

>	eqBE:=Q=m*c*DT;eqBE1:=T1=T0+Q/(m*c);

b) Perfil de temperatura a lo largo del conducto.

(Ver arriba.)

c) Temperatura de salida del conducto, T2, (en función del gasto másico de agua).

>	eqBE2:=dH/dt=Qcond+Qconv+Qwall;eqBE2:=m*c*diff(T(x),x)=k*Pi*R^2*diff(T(x),x,x)-K*2*Pi*R*(T(x)-T0);eqBE2:=m*c*diff(T(x),x)=-K*2*Pi*R*(T(x)-T0);dsol1:=subs(eqBE1,dsolve({eqBE2,T(0)=T1},T(x)));eq2:=subs(T(x)=T2,x=L,dsol1);

d) Gasto másico que daría máxima temperatura de salida del conducto y valor de ésta.

Si m es pequeño se calienta mucho pero pierde mucho también; si m es grande se calienta menos pero pierde menos.

>	m_Tm=T2(m)[max];m_Tm:=solve(diff(rhs(eq2),m)=0,m);m_Tm_:=evalf(subs(dat,m_Tm));T2m:=subs(m=m_Tm,rhs(eq2));T2m_:=evalf(subs(dat,T2m));

Si representamos la temperatura tras el calentador, T1, y la del extremo de salida, T2, en función del gasto de agua:

>	plot(subs(dat,SI0,{rhs(eqBE1),rhs(eq2),subs(dat,SI0,[[0,T0],[1,T0]])}),m=0..0.1,Temp=0..500,color=black);

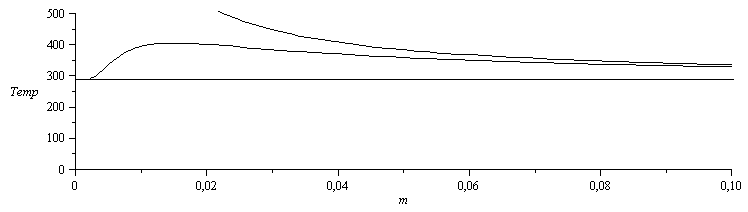No es realista esa Tmax, que habrá de ser menor que la de ebullición a presión ambiente. En realidsad, para agua caliente sanitaria basta conque T2=45 ºC ( y la T1 tampoco puede ser mayor de unos 100 ºC para evitar la formación de vapor).

e) Comentar la viabilidad y conveniencia del punto de trabajo anterior.

Efectivamente, vemos que no es realista considerar gastos másicos pequeños; un gasto típico de un grifo es ya 0,1 kg/s (6 L/min).

>