>	restart:#"m11_p15"

El modelo de transmisión de calor para el calentamiento de agua en una olla de aluminio sobre una placa de hierro (cocina) expuesta a la llama de un hogar es el siguiente. Se supone flujo unidimensional (vertical); la parte inferior del hierro se supone a 600 °C, el espesor de hierro es de 5 mm y su conductividad k=50 W.m­1.K­1; debido al mal contacto físico entre la placa y la olla, se supone que existe una capa de 50 µm de aire (k=0,02 W.m­1.K­1) entre ellas; el espesor de aluminio de la olla es de 2 mm y su conductividad k=200 W.m­1.K­1; el coeficiente de convección térmica con el agua, que está en ebullición con una temperatura lejos del fondo de 100 °C, se supone que es de 4000 W.m­2.K­1. Se pide:
 1.Esquema del perfil de temperatura.
 2.Cálculo del flujo unitario de calor.
 3.Cálculo de las temperaturas intermedias.
 4.Corrección correspondiente a tomar una dependencia de la forma k/T1/2=cte para la conductividad del aire.

Datos:

>	read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):

>	su1:="Aluminio_anodizado":su2:="Hierro_fundido":su3:="Aire":su4:="H2O": dat:=[T[1]=(273+600)*K_,L[1]=0.005*m_,k[1]=50*W_/(m_*K_),L[2]=50e-6*m_,k[2]=0.02*W_/(m_*K_),L[3]=0.002*m_,k[3]=200*W_/(m_*K_),T[5]=(273+100)*K_,h=4000*W_/(m_^2*K_),k=cte*sqrt(T)];

>	dat:=op(dat),Const,SI2,SI1:Aldat:=get_sol_data(su1):Idat:=get_sol_data(su2):Adat:=get_gas_data(su3):Wdat:=get_liq_data(su4):qCheck_kI:=subs(dat,k[1])=subs(Idat,k);eqCheck_kA:=subs(dat,k[2])=subs(Adat,k);eqCheck_kAl:=subs(dat,k[3])=subs(Aldat,k);eqCheck_Tb:=subs(dat,T[5])=subs(Wdat,T[b]);

a) .Esquema del perfil de temperatura

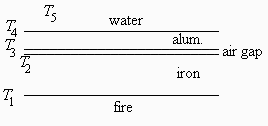
b) Cálculo del flujo unitario de calor.

>	eq1:=dsolve(subs(phi=0,eq11_6_10),T(x));eq2:=eval(subs(eq1,eq11_1));eq3:=q=(T[5]-T[1])/(L[1]/k[1]+L[2]/k[2]+L[3]/k[3]+1/h);eq3_:=subs(dat,eq3);

i.e. fluyen 170 kW/m2.

c) Cálculo de las temperaturas intermedias.

>	eq31:=q=(T[2]-T[1])/(L[1]/k[1]);eq32:=q=(T[3]-T[2])/(L[2]/k[2]);eq33:=q=(T[4]-T[3])/(L[3]/k[3]);eq34:=q=(T[5]-T[4])/(1/h);sol3:=solve({eq31,eq32,eq33,eq34},{q,T[2],T[3],T[4]});sol3_:=subs(dat,sol3);

i.e. desde los 873 K de abajo, 855 K sobre el hierro, 418 K bajo el aluminio y 416 K encima, estando el agua hirviendo a 373 K fuera de la capa límite.

Nótese el enorme salto térmico en la delgada capa de aire.

>

T12:=subs(sol3_,dat,SI0,T[1]+(T[2]-T[1])*(x-0)/L[1]);T23:=subs(sol3_,dat,SI0,T[2]+(T[3]-T[2])*(x-L[1])/L[2]);T34:=subs(sol3_,dat,SI0,T[3]+(T[4]-T[3])*(x-L[1]-L[2])/L[3]);T45:=subs(sol3_,dat,SI0,T[5]+(T[4]-T[5])*exp(-1e3*(x-L[1]-L[2]-L[3])));plot(subs(dat,SI0,{[x,T12,x=0..0.005],[x,T23,x=0.005..0.00505],[x,T34,x=0.00505..0.007],[x,T45,x=0.007..0.01],[[0,0],[0,1000]],[[L[1],0],[L[1],1000]],[[L[1]+L[2],0],[L[1]+L[2],1000]],[[L[1]+L[2]+L[3],0],[L[1]+L[2]+L[3],1000]],[[0.007,T[5]],[1,T[5]]]}),x=0..0.01,0..1000,color=black);

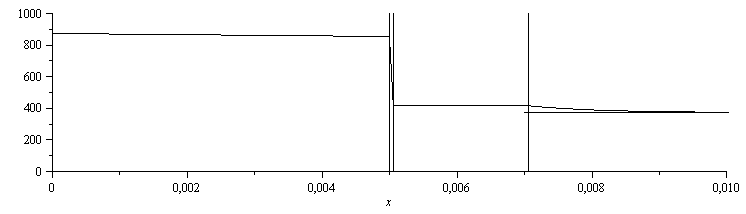d) Corrección correspondiente a tomar una dependencia de la forma k/T1/2=cte para la conductividad del aire.

Para cada una de las temperaturas:

>	cte_:=solve(subs(dat,T=T0,dat,k=k[2]),cte):'cte'=evalf(%,2);k0_:=evalf(subs(dat,T=T0,dat,sol3_,cte=cte_,k)):'k0'=evalf(%,2);k2_:=subs(dat,T=T[2],sol3_,cte=cte_,k):'k2'=evalf(%,2);k3_:=subs(dat,T=T[3],sol3_,cte=cte_,k):'k3'=evalf(%,2);

Si se toma una k media entre las dos temperaturas correspondientes:

>	k_:=(k2_+k3_)/2;sol3__:=subs(k[2]=k_,dat,sol3):evalf(%,2);

Nótese la gran importancia de la modelización adecuada de la capa de aire: el calor es ahora de 240 kW/m2 en vez de 170 kW/m2.

Si se hace exacto:

>

eqBE:=0=diff(subs(dat,T=T(x),k)*diff(T(x),x),x);dsol1:=dsolve(eqBE,T(x),explicit)[3];eqq:=q=subs(dat,T=T(x),k)*diff(T(x),x);eqq_:=dsolve(eqq,T(x));eqT:=T23_=((-(2/3)*T[2]^(3/2)*cte+q*(L[1]-x))*(-3/2))*(2/3);eqq__:=q=solve(subs(T(x)=T[3],x=L[1]+L[2],eqq_)-subs(T(x)=T[2],x=L[1],eqq_),q);sol3_:=fsolve(subs(cte=cte_,dat,SI0,{eq31,eqq__,eq33,eq34}),{q,T[2],T[3],T[4]},{T[2]=400..1000,T[3]=400..1000,T[4]=400..1000});

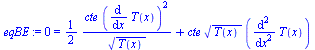luego era buena la aproximación anterior.

>