Se trata del estudio del perfil de temperatura en régimen periódico en un estanque de agua en reposo, en contacto con una atmósfera gaseosa cuya temperatura varía según la ley T∞=Tm+Tsin(2t/), con Tm=5 °C y un coeficiente de convección h=10 W∙m 2∙K 1, en función de T y . En particular, se desea conocer el T mínimo para la formación de hielo en los casos =1 hora, =1 día y =1 mes.
Datos:
| > |
read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):assume(m_>0): |
| > |
su:="H2O":dat:=[Tma=(5+273)*K_,h=10*W_/(m_^2*K_),tau1=3600*s_,tau2=86400*s_,tau3=30*86400*s_,tau4=365*86400*s_];eqdat:=Tinf=Tma+DTa*sin(2*Pi*t/tau); |
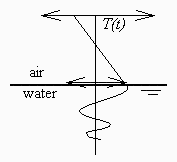
| > |
dat:=op(dat),get_liq_data(su),Const,SI1,SI2: |
Se desea conocer el T mínimo para la formación de hielo en los casos =1 hora, =1 día y =1 mes.
Se trata de un problema de excitación periódica. Se conoce la solución para condición de Dirichlet (i.e. fijando T(0,t)):
| > |
subs(DT=DT0,eq11_23);eqteo:=T0=eval(subs(x=0,rhs(%))); |
Pero en este caso lo que se sabe es la q(0,t) (condición de Newman) y no la T(0,t)=T0(t). Podemos pasar de una a otra con el balance en la entrefase: (por supuesto que en todo momento se supone que no hay cambio de fase; es el caso límite el que interesa).
| > |
eqBE:=h*(Tinf-T0)=-k*diff(T(x,t),x);eqBE:=subs(eqdat,eqteo,h*(Tinf-T0))=eval(subs(t=t-t0,x=0,eval(subs(eq11_23,DT=DT0,-k*diff(T(x,t),x))))); |
i.e. el efecto de la convección lo que hace es disminuir la amplitud de las oscilaciones e introducir un retraso:
| > |
eq0:=h*(Tma-T[mean])=0;eq0_:=T[mean]=Tma;eqsin:=h*(DTa-DT0)=k*DT0*sqrt(Pi/(a*tau))*(cos(2*Pi*t0/tau)-sin(2*Pi*t0/tau));eqsin_:=DT0_=solve(%,DT0);eqcos:=0=k*DT0*sqrt(Pi/(a*tau))*(-sin(2*Pi*t0/tau)-cos(2*Pi*t0/tau));eqcos_:=t0=solve(%,t0); |
Como sólo interesa cuando empieza a formarse hielo, bastará estudiar cuándo se alcanzan los 0 ºC en la superficie, es decir, cuando la amplitud es de 5 ºC, como la media.
| > |
eq_ice:=DT0=Tma-T[f];DTa_:=solve(rhs(eqsin_)=Tma-T[f],DTa);DTa_1:=evalf(subs(a=k/(rho*c),eqcos_,tau=tau1,dat,SI0,DTa_))*K_;DTa_2:=evalf(subs(a=k/(rho*c),eqcos_,tau=tau2,dat,SI0,DTa_))*K_;DTa_3:=evalf(subs(a=k/(rho*c),eqcos_,tau=tau3,dat,SI0,DTa_))*K_;DTa_4:=evalf(subs(a=k/(rho*c),eqcos_,tau=tau4,dat,SI0,DTa_))*K_; |
i.e. bastarían 5,33 ºC de amplitud de oscilación de la temperatura del aire sobre 5 ºC de media, para que empezase a helarse el agua si la oscilación fuese anual, pero si la oscilación es más rápida, se admite más porque se amortigua; e.g. si el periodo es diario, el aire debe llegar a 5-11,7=-6,7 ºC para que empiece a helarse el agua.
| > |
sin(Pi*(t-t0))=expand(sin(Pi*(t-t0)));cos(Pi*(t-t0))=expand(cos(Pi*(t-t0))); |
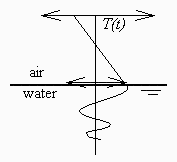
![T(x, t) = `+`(T[mean], `*`(DT0, `*`(exp(`+`(`-`(`/`(`*`(x), `*`(`^`(`/`(`*`(a, `*`(tau)), `*`(Pi)), `/`(1, 2))))))), `*`(sin(`+`(`/`(`*`(2, `*`(Pi, `*`(t))), `*`(tau)), `-`(`/`(`*`(x), `*`(`^`(`/`(`*`...](images/p14_4.gif)
![`*`(h, `*`(`+`(Tma, `*`(DTa, `*`(sin(`+`(`/`(`*`(2, `*`(Pi, `*`(t))), `*`(tau)))))), `-`(T[mean]), `-`(`*`(DT0, `*`(sin(`+`(`/`(`*`(2, `*`(Pi, `*`(t))), `*`(tau)))))))))) = `+`(`-`(`*`(k, `*`(`+`(`-`(...](images/p14_7.gif)
