>	restart:#"m11_p12"

Considérese una fuente volumétrica de energía de intensidad 0exp[(TT0)] por unidad de volumen. Determinar bajo qué condiciones se alcanzaría un régimen estacionario cuando el contorno está a T0 en los casos siguientes:
a) Pared plana de espesor L y conductividad infinita y coeficiente de convección h.
b) Cilindro de radio R y conductividad infinita y coeficiente de convección h.
c) Esfera de radio R y conductividad infinita y coeficiente de convección h.
d) Pared plana de espesor L y conductividad k.
e) Cilindro de radio R y conductividad k.
f) Esfera de radio R y conductividad k.Datos:

>	read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):assume(theta>0,t>=theta):

>	dat:=[phi=phi0*exp(beta*(T(x)-T0))];assume(x>=0,r>=0,T0>0,beta>0,p>0,q0>0):

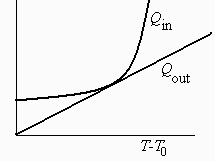
a) Pared plana de espesor L y conductividad infinita y coeficiente de convección h.

La solución será crítica cuando la recta del enfriamiento sea tangente a la de calentamiento (Qin=Qout).

Del análisis dimensional se deduce que sólo hay un parámetro adimensional: p=phi0*beta*L/h.

>

deq1:=m*c*dT/dt=Qin-Qout;deq1:=m*c*dT/dt=V*phi-h*Area*(T-T0);deq1:=rho*A*L*c*diff(T(t),t)=A*L*subs(dat,T(x)=T(t),phi)-h*2*A*(T(t)-T0);eqp:=p=phi0*beta*L/h;Tp1:=subs(T(t)=T,op([2,1],deq1));Tp2:=-subs(T(t)=T,op([2,2],deq1));DTp1:=diff(Tp1,T);DTp2:=diff(Tp2,T);eq1:=DTp1/Tp1=DTp2/Tp2;sol1:=solve({Tp1=Tp2,DTp1=DTp2},{T,h});eqp_:=subs(sol1,eqp);evalf(%);

i.e. el sistema explotará si p>0,74 por enfriamiento insuficiente.

b) Cilindro de radio R y conductividad infinita y coeficiente de convección h.

>

eqp:=p=phi0*beta*R/h;deq1:=rho*c*Pi*R^2*L*diff(T(t),t)=Pi*R^2*L*subs(dat,T(x)=T(t),phi)-h*2*Pi*R*L*(T(t)-T0);Tp1:=subs(T(t)=T,op([2,1],deq1));Tp2:=-subs(T(t)=T,op([2,2],deq1));DTp1:=diff(Tp1,T);DTp2:=diff(Tp2,T);eq1:=DTp1/Tp1=DTp2/Tp2;sol1:=solve({Tp1=Tp2,DTp1=DTp2},{T,h});eqp_:=subs(sol1,eqp);evalf(%);

i.e. el sistema explotará si p>0,74 por enfriamiento insuficiente.

c) Esfera de radior R y conductividad infinita y coeficiente de convección h.

>	deq1:=rho*c*(4/3)*Pi*R^3*diff(T(t),t)=Pi*(4/3)*Pi*R^3*subs(dat,T(x)=T(t),phi)-h*4*Pi*R^2*(T(t)-T0);Tp1:=subs(T(t)=T,op([2,1],deq1));Tp2:=-subs(T(t)=T,op([2,2],deq1));DTp1:=diff(Tp1,T);DTp2:=diff(Tp2,T);eq1:=DTp1/Tp1=DTp2/Tp2;sol1:=solve({Tp1=Tp2,DTp1=DTp2},{T,h});eqp_:=subs(sol1,eqp);evalf(%);

i.e. el sistema explotará si p>0,35 por enfriamiento insuficiente.

d) Pared plana de espesor L y conductividad k.

>	deq:=subs(dat,eq11_6_10);#dsolve({deq,T(0)=T0,T(L)=T0},T(x));

Hay que hacerlo numéricamente.

>

with(DEtools): deq1:=expand(Dchangevar(T(x)=T0+ln(theta(xi))/beta,x=L*xi,phi0=p*k/(beta*L^2),deq,x,xi)*L*L*beta*theta(xi)^2);eq1:=diff(theta(xi),xi)=q(theta(xi));eq2:=diff(eq1,xi);deq2:=subs(eq2,eq1,theta(xi)=theta,deq1);dsol1:=dsolve({deq2,q(1)=q0},q(theta));deq3:=subs(theta=theta(xi),q(theta(xi))=diff(theta(xi),xi),dsol1);eq3:=0=subs(theta(xi)=theta,rhs(deq3))/theta;tmax:=expand(solve(eq3,theta));int_:=subs(theta(xi)=theta,1/rhs(deq3));eq1:=xi=Int(int_,theta);eq1_:=1/2=int(int_,theta=1..tmax);

>	with(plots):implicitplot(eq1_,q0=.1..10,p=.1..10);

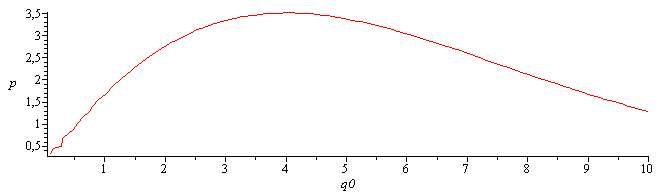>	eq1d_:=subs(p(q0)=p,diff(subs(p=p(q0),eq1_),q0)):sol1:=fsolve({eq1_,eq1d_},{p,q0},{p=0..10,q0=0..10}):evalf(%,2);tmax_:=subs(sol1,tmax)*s_:'tmax'=evalf(%,2);xi:=evalf(int(subs(sol1,int_),theta=1..t));

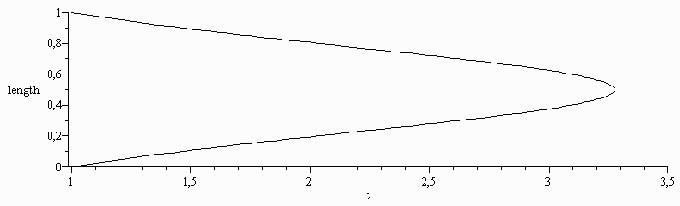
e) Cilindro de radio R y conductividad k.

NO ES AUTÓNOMO.

f) Esfera de radior R y conductividad k.

NO ES AUTÓNOMO