>	restart:#"m11_p11"

Una pared de hormigón de 0,5 m de espesor está en una atmósfera a 300 K y a partir de un cierto instante empieza a recibir una irradiación de 500 W/m2 que absorve en su totalidad. Se pide:
 1.Perfil de temperatura estacionario suponiendo que las pérdidas son por convección con h=10 W.m­2.K­1.
 2.Perfil de temperatura estacionario suponiendo que las pérdidas son por convección con h=10 W.m­2.K­1 y por radiación como cuerpo negro.
 3.Evolución del perfil de temperatura en régimen transitorio.

Datos:

>	read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):

>	su:="Hormigon":dat:=[L=0.5*m_,T0=300*K_,E=500*W_/m_^2,h=10*W_/(m_^2*K_)];

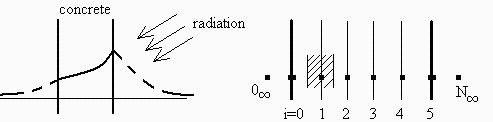
Eqs. const.:

>	sdat:=[get_sol_data(su)]:dat:=op(dat),op(subs(epsilon=epsilon_,sdat)),Const,SI2,SI1:k=subs(dat,k);

a) Perfil de temperatura estacionario suponiendo que las pérdidas son por convección con h=10 W.m­2.K­1.

Se plantean sendos balances energéticos en las entrefases:

>	eq1:=h*(T[1]-T0)+epsilon*sigma*(T[1]^4-T0^4)=k*diff(T(x),x);eq2:=E=k*diff(T(x),x)+h*(T[2]-T0)+epsilon*sigma*(T[2]^4-T0^4);T(x):=T[1]+(T[2]-T[1])*x/L;sol1:=solve(subs(epsilon=0,{eq1,eq2}),{T[1],T[2]});sol1_:=expand(subs(dat,sol1));T[1]=TKC(subs(sol1_,T[1]));T[2]=TKC(subs(sol1_,T[2]));

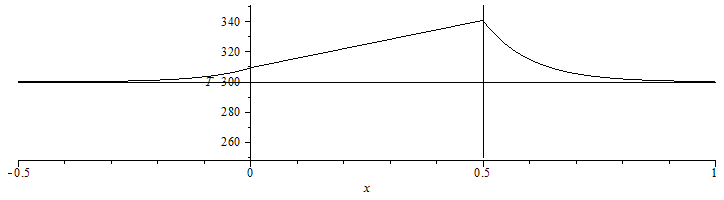
i.e., la cara irradiada se pone a 67 ºC y la otra a 36 ºC (en un ambiente a 27 ºC).

Se puede dibujar a escala todo el perfil de temperaturas si se aproximan las capas límite (e.g. por exponenciales empíricas):

>

T01:=subs(sol1_,dat,SI0,T0+(T[1]-T0)*exp(1e1*x));T12:=subs(dat,sol1_,SI0,T(x));T23:=subs(sol1_,dat,SI0,T0+(T[2]-T0)*exp(-1e1*(x-L)));plot({[x,T01,x=-0.5..0],[x,T12,x=0..0.5],[x,T23,x=0.5..1],[x,subs(dat,SI0,T0),x=-0.5..1],subs(dat,SI0,[[0,0],[0,1000]]),subs(dat,SI0,[[L,0],[L,1000]])},x=-0.5..1,'T'=250..350,color=black);

b) Perfil de temperatura estacionario suponiendo que las pérdidas son por convección con h=10 W.m­2.K­1 y por radiación como cuerpo negro.

>	eq1;eq2;sol1_:=fsolve(subs(epsilon=1,dat,SI0,{eq1,eq2}),{T[1],T[2]}):T1_:=subs(sol1_,T[1])*K_;T[1]=TKC(%);T2_:=subs(sol1_,T[2])*K_;T[2]=TKC(%);

i.e., la cara irradiada se pone ahora a 53 ºC (en vez de a 67 ºC) y la otra a 31 ºC (en vez de a 36 ºC).

ADICIONAL. Ya puestos, podemos ver el efecto de la emisividad en todo el rango de 0 a 1.

>

eqd1:=0=convert(series(subs(T[1]=T0+DT1,T[2]=T0+DT2,rhs(eq1)-lhs(eq1)),DT1=0,2),polynom);DT1_:=solve(eqd1,DT1);eqd2:=0=convert(series(subs(T[1]=T0+DT1,T[2]=T0+DT2,rhs(eq2)-lhs(eq2)),DT2=0,2),polynom);DT2_:=solve(subs(DT1=DT1_,eqd2),DT2);DT2__:=evalf(subs(dat,SI0,k=1.5,DT2_));DT2_e0:=subs(epsilon=0,DT2__)*K_;DT2_e1:=subs(epsilon=1,DT2__)*K_;plot(DT2__,epsilon=0..1,DT2=0..50,color=black);

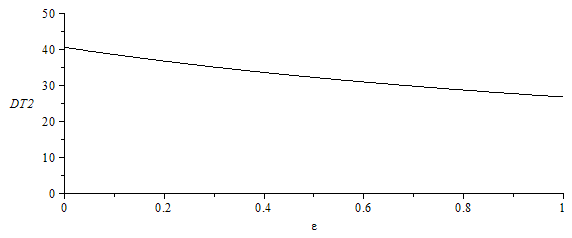i.e. el efecto es casi lineal calentándose 41 ºC si no emite y 27 ºC si emite perfectamente.

c) Evolución del perfil de temperatura en régimen transitorio.

Hay que discretizar y calcular numéricamente.

Sea N el nº de capas (ver Fig. 1) y M el nº de intervalos de tiempo.

El intervalo espacial es Dx=L/N.

El intervalo temporal Dt lo elegiremos para que Fo<1/2; e.g. Fo=1/4.

La discretización es:

>

eq11_24;eq_i:=subs(phi=0,h[lat]=0,epsilon[lat]=0,eq11_24_gen_);eq_0:=subs(phi=0,h[lat]=0,epsilon[lat]=0,h0=h,epsilon0=1,E0=0,eq11_24_0_);eq_N:=subs(phi=0,h[lat]=0,epsilon[lat]=0,hN=h,epsilonN=1,EN=E,eq11_24_N_);eqFo:=Fo=a*Dt/Dx^2;eqa:=eq11_5;eqDx:=Dx=L/N;eqDt:=Dt=solve(subs(eqFo,eqa,eqDx,0.25=rhs(eqFo)),Dt);

Para los valores numéricos, además de los datos, se elige un valor de N del orden de 10 (i.e. aproximar una curva por diez puntos intermedios), de donde se deduce Dx y Dt (para que sea estable). Para llegar hasta el régimen estacionario, o se compara a cada paso la solución para ver cuándo ya no varía apreciablemente, o se estima por otro método el tiempo de relajación, o simplemente se calcula un número grande ve pasos y después se ve si se había estabilizado.

>	N:=10;M:=1000;datnum0:=op(subs(SI0,[Dt=subs(dat,rhs(eqDt)),Dx=subs(dat,rhs(eqDx)),Fo=subs(Dt=rhs(eqDt),eqa,eqDx,dat,rhs(eqFo)),dat]));

Inicialización: T[i , j=0]=T0.

>	j:=0:for i from 0 to N do T[i,j]:=subs(datnum0,T0):od:

Iteraciones.

>	for j from 0 to M-1 do eq_0_:=subs(datnum0,eq_0);assign(%); for i from 1 to N-1 do eq_i_:=subs(datnum0,eq_i);assign(%);od; eq_N_:=subs(TN=T0,datnum0,eq_N);assign(%);od:

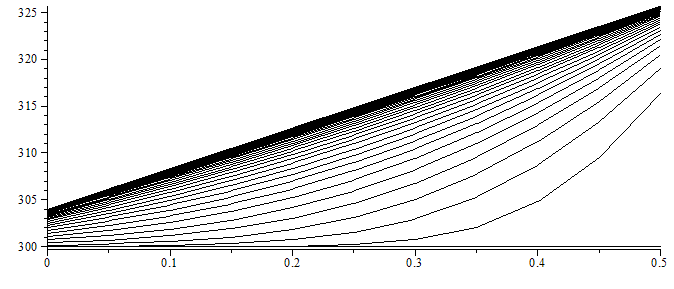
Resultado.

>	Mdis:=99:pl:=subs(datnum0,[seq([seq([L*(i/N),T[i,jdis*trunc(M/Mdis)]],i=0..N)],jdis=0..Mdis)]):plot(pl,color=black);

>	plot(subs(datnum0,[seq([seq([subs(datnum0,M*Dt)*(j/M),T[i,j*trunc(M/Mdis)]],j=1..Mdis)],i=1..N)]),color=black);

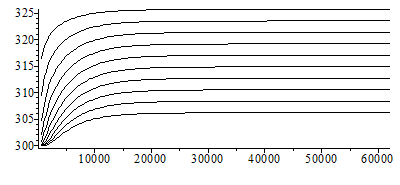Visualización interactiva:

>	with(plots): Ts :=subs(datnum0,[seq([seq([L*(i/N),j*Dt,T[i,j]],i=0..N)],j=1..M)]): surfdata( Ts, axes=boxed, style=patch,labels=[`L`,`time`,`Temp`] );

>
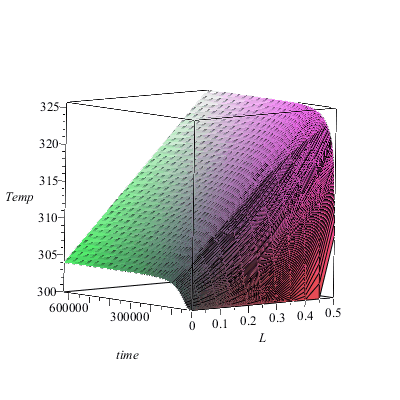