>	restart:#"m11_p08"

La pared de un horno de tratamientos térmicos tiene una conductividad térmica k=0,7 W.m­2.K­1, una densidad r=1200 kg.m­3, una capacidad térmica c=1130 J.kg­1.K­1 y 20 cm de espesor. Para un cierto proceso se necesita que la temperatura interior varíe cíclicamente entre 100 °C y 750 °C cada 3 horas. Se pide:
 1.Modelización del problema.
 2.Amplitud de la variación de temperatura en la cara externa.
 3.Retraso de la onda térmica.

Datos:

>	read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):

>	dat:=[k=0.7*W_/(m_*K_),rho=1280*kg_/m_^3,c=1130*J_/(kg_*K_),L=0.2*m_,Tmin=(273+100)*K_,Tmax=(273+750)*K_,tau=3*3600*s_];dat:=op(dat),Const,SI2,SI1:

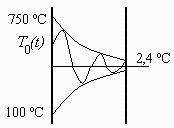
a) Modelización del problema.

La conducción unidimensional en un medio homogéneo semiinfinito cuya superficie libre está sometida a oscilaciones periódicas de temperatura en la forma T0(t)=Tmean+DT*sen(2*Pi*t/tau). La solución periódica de la ecuación del calor es:

>

eq11_23;

Las oscilaciones se van amortiguando y para x >>(a*tau/Pi)^1/2 ya apenas varía (así que aunque se haya desarrollado para un medio semiinfinito, vale para paredes de espesor mucho mayor que el antedicho). Es de destacar el retraso en fase que se introduce al penetrar la onda térmica, pues lo hace con velocidad finita constante e igual a 2(Pi*a/tau)^1/2.

b) Amplitud de la variación de temperatura en la cara externa.

>	DT:=DT0*exp(-x/sqrt(a*tau/Pi));DT0:=Tmax-Tmin;a:=k/(rho*c);a_:=subs(dat,SI2,a);DT_:=evalf(subs(dat,a=a_,SI2,DT));DT_L_:=evalf(subs(x=L,dat,SI0,DT_))*K_;plot(subs(dat,SI0,DT_),x=0..0.2,0..650);

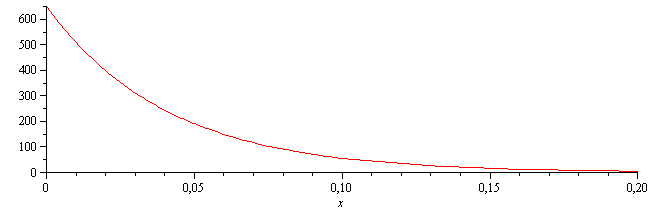i.e., la amplitud interna de (750-100)=650 ºC se reduce a unos escasos 5 K en la cara exterior.

c) Retraso de la onda térmica.

>	eqt:=t[ret]=x*tau/(2*Pi*sqrt(a*tau/Pi));eqt_:=subs(dat,evalf(subs(dat,%)));eqtL:=subs(x=L,dat,%);plot(subs(eqt_,dat,SI0,t[ret])/3600,x=0..0.2,horas=0..3);

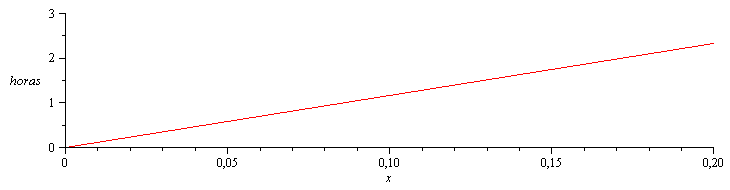i.e., la onda térmica llega con un desfase de unos 8400 s a la cara externa (unas 2,3 h, comparado con las 3 h del ciclo).

>