>	restart:#"m11_p05"

Una aleta rectangular de aluminio tiene 1 mm de espesor, 50 mm de longitud y 100 mm de anchura. La temperatura en la raiz es de 130 °C y el coeficiente de convección con el aire atmosférico es h=50 W.m­2.K­1. Determinar:

a) El perfil de temperatura.

b) El flujo de calor.

c) El rendimiento de la aleta.

Datos:.

>	read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):assume(x>0):

>	su:="Aluminio_anodizado":dat:=[a=0.001*m_,L=0.050*m_,b=0.100*m_,Troot=(130+273)*K_,h=50*W_/(m_^2*K_),Tinf=T0];

>	dat:=op(dat),get_sol_data(su),Const,SI2,SI1:

Teoría básica de aletas. Solución general estacionaria. Caso de un extremo fijo y otro aislado (flujo de calor despreciable).

>	eq11_12;eq11_13;eq11_14;eqEst:=subs(T(x)=T,dsolve(subs(T[infinity]=Tinf,eq11_14),T(x)));eqEst_0_inf:=dsolve({subs(T[infinity]=Tinf,eq11_14),T(0)=T0,D(T)(L)=0},T(x)):expand(convert(%,trig)):eqEst_0_inf:=eq11_15;

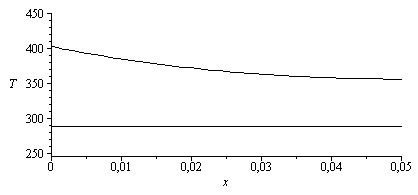
a) El perfil de temperatura.

>	T_:=Tinf+(Troot-Tinf)*cosh(m*(L-x))/cosh(m*L);eqp:=p=2*(a+b);subs(dat,%);eqA:=A=a*b;subs(dat,%);eqm:=m=evalf(subs(eqp,eqA,dat,rhs(eq11_13)));eqm:=m=subs(SI0,rhs(%))/m_;plot(subs(eqm,dat,SI0,[T_,T0]),x=0..subs(dat,L/m_),T=250..450,color=black);

b) El flujo de calor.

A través de la raiz:

>	eqQ:=Q[root]=-k*A*diff(T(x),x);eqQ_:=subs(x=0,eval(subs(T(x)=T_,%)));eq11_16;eqQ__:=evalf(subs(eqA,eqm,dat,eqQ_)):subs(dat,%);

i.e., se evacuan 42 W por la aleta.

c) El rendimiento de la aleta.

Respecto a aleta isoterma a Troot:

>	eq11_16_1;eq11_16_2;evalf(subs(eqm,dat,%));

Respecto al área en la raiz:

>	eq11_16_3;eq11_16_4;evalf(subs(eqm,eqA,eqp,dat,%));

i.e., la aleta elimina 73 veces más de calor que si no estuviera más que el área raiz, y un 72% del calor que disiparía si estuviese toda a la temperatura máxima.

>