>	restart:#"m11_p04"

Para mover un eje a 1000 rpm en un cojinete de fricción, de bronce, de 60 mm de agujero, 100 mm de diámetro exterior y 500 mm de ancho, se necesita un par de 10 N.m para vencer el rozamiento. Calcular:
a) La potencia consumida.
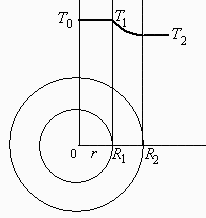
b) El perfil de temperatura en función de la temperatura exterior.

Datos:

>	read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):assume(x>0):

>	su:="Bronce":dat:=[Omega=1000/60*2*Pi/s_,R[1]=0.030*m_,R[2]=0.050*m_,L=0.5*m_,M=10*N_*m_];

>	sdat:=get_sol_data(su):dat:=op(dat),sdat:

a) La potencia consumida.

El eje debe ser isotermo porque no puede evacuar calor hacia dentro, luego toda la energía disipada ha de ir hacia afuera.

>	Phi:=M*Omega;Phi_:=subs(SI1,evalf(subs(dat,SI2,Phi)));

i.e., se disipan unos 1050 W.

b) El perfil de temperatura en función de la temperatura exterior.

O se aplican directamente las fórmulas del caso, o se deducen (como aquí):

>	eqHE:=subs(phi=0,eq11_6_20);expand(dsolve(%,T(r)));eq11_11_2_;eq11_11_2;eqphi:=phi=M*Omega/(2*Pi*R[1]*L);subs(dat,evalf(subs(dat,%)));evalf(subs(R[0]=R[1],R[ext]=R[2],eqphi,dat,SI2,eq11_11_2));

i.e. la entrefase friccionante se calienta 3 K más de la temperatura exterior.

>