>	restart;#'therm_eq11.mw'.

Chapter 11: Set of pre-written equations available. We use Q and q instead of Qdot and qdot.

Fourier's law (constitutive equation)

>	with(linalg):eq11_1:=q=-k*diff(T(x),x);eq11_1_0:=q=-k*grad(T(x,y,z),[x,y,z]);eq11_1_1:=q=-k*grad(T(r,theta,z,t),[r,theta,z],coords=cylindrical);eq11_1_2:=q=-k*grad(T(r,theta,phi,t),[r,theta,phi],coords=spherical);

Warning, the protected names norm and trace have been redefined and unprotected

Newton's law of heat transfer: unitary convection, global convection and global transfer:

>	eq11_2:=q=h*DT;eq11_2_0:=Q=h*A*DT;eq11_2_1:=Q=K*A*DT;eq11_2_2:=Q=K*A*(T[infinity]-T);

Stefan's law of heat transfer by radiation:

>	eq11_3:=Q=epsilon*A*sigma*(T[0]^4-T^4);

Energy balance at constant p. From control mass to unit control volume with Gauss-Ostrogradski's theorem:

>	eq11_4:=dH/dt=Qnet;eq11_4_1:=m*c*dT/dt=Qnet;eq11_4_2:=rho*diff(h(t),t)=-diverge([q[x](x,y,z),q[y](x,y,z),q[z](x,y,z)],[x,y,z]);

Definition of thermal diffusivity:

>	eq11_5:=a=k/(rho*c);

Heat equation (homogeneous, no sources):

>

eq11_5_1:=rho*c*diff(T(x,y,z,t),t)=k*laplacian(T(x,y,z),[x,y,z]);eq11_5_2:=T[t]=a*(T[xx]+T[yy]+T[zz]);eq11_5_3:=rho*c*diff(T(r,theta,z,t),t)=k*laplacian(T(r,theta,z),[r,theta,z],coords=cylindrical);eq11_5_4:=T[t]=a*(T[rr]+T[r]/r+T[theta,theta]/r^2+T[zz]);eq11_5_5:=rho*c*diff(T(r,theta,phi,t),t)=k*laplacian(T(r,theta,phi),[r,theta,phi],coords=spherical);eq11_5_6:=T[t]=a*(T[rr]+2*T[r]/r+T[theta,theta]/r^2+cot(theta)*T[theta]/r^2+T[phi,phi]/(r*sin(theta))^2);

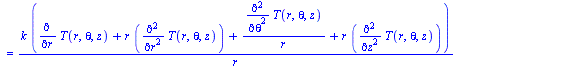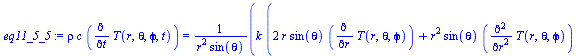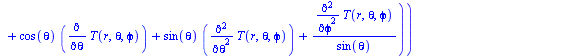Heat eq. 1D-planar, with uniform sources, steady & unsteady

>	eq11_6_10:=0=subs(i=0,r=x,(i/r)*diff(T(r),r)+diff(T(r),r,r))+phi/k;eq11_6_11:=diff(T(x,t),t)=a*diff(T(x,t),x,x)+phi/(rho*c);

Heat eq. 1D-cyl, with uniform sources, steady & unsteady. Also 2D-polar and 2D-axial.

>

eq11_6_20:=0=subs(i=1,(i/r)*diff(T(r),r)+diff(T(r),r,r))+phi/k;eq11_6_21:=diff(T(r,t),t)=expand(a*subs(i=1,(i/r)*diff(T(r,t),r)+diff(T(r,t),r,r))+phi/(rho*c));eq11_6_22_polar:=diff(T(r,theta,t),t)=a*laplacian(T(r,theta,t),[r,theta],coords=polar)+phi/(rho*c);eq11_6_22_axial:=diff(T(r,z,t),t)=a*(diff(r*diff(T(r,z,t),r),r)/r+diff(T(r,z,t),z,z))+phi/(rho*c);

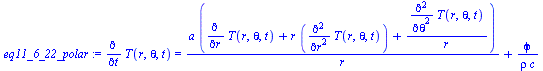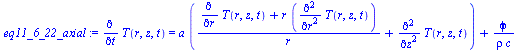Heat eq. 1D-spherical, with sources, steady & unsteady

>	eq11_6_30:=0=subs(i=2,(i/r)*diff(T(r),r)+diff(T(r),r,r))+phi/k;eq11_6_31:=diff(T(r,t),t)=expand(a*subs(i=2,(i/r)*diff(T(r),r)+diff(T(r),r,r))+phi/(rho*c));

Definition of thermal resistance R, and some particular values for 1D: planar, cyl., sph.:

>	eq11_7:=Q=DT/R;eq11_7_1:=Q=k*A*DT/L,R=L/(k*A);eq11_7_2:=Q=k*2*Pi*L*DT/ln(R[2]/R[1]),R=ln(R[2]/R[1])/(2*k*Pi*L);eq11_7_3:=Q=k*4*Pi*R[1]*R[2]*DT/(R[2]-R[1]),R=(R[2]-R[1])/(k*4*Pi*R[1]*R[2]);

Steady 1D planar symmetric with uniform source: T(x) and total Q (NOTICE that center is at L/2, and only Q/2 flows at one end):

>	eq11_8_1:=T(x)=T[1]+(phi*L^2/(8*k))*(1-(2*x/L)^2);eq11_8_2:=Q=A*phi*L;

Steady 1D cylindrical symmetric with uniform source: T(r) and total Q

>	eq11_9_1:=T(r)=T[1]+(phi*R^2/(4*k))*(1-(r/R)^2);eq11_9_2:=Q=phi*Pi*R^2*L;

Steady 1D spherical symmetric with uniform source: T(r) and total Q:

>	eq11_10_1:=T(r)=T[1]+(phi*R^2/(16*k))*(1-(r/R)^2);eq11_10_2:=Q=(4/3)*phi*Pi*R^3;

Interfacial sources in 1D, planar: between two equal walls of depth L:

>	eq11_11_1_:=T(x)=T[L]+(phi*L/(2*k))*(1-x/L);eq11_11_1:=T[0]=T[L]+(phi*L/(2*k));

Interfacial sources in 1D,cyl: at R[0] (T(r)=T[R[0]] for r<R[0]):

>	eq11_11_2_:=T(r)=T[R[ext]]+(phi*r/k)*ln(R[ext]/r);eq11_11_2:=T[R[0]]=T[R[ext]]+(phi*R[0]/k)*ln(R[ext]/R[0]);

Interfacial sources in 1D,spherical: at R[0] (T(r)=T[R[0]] for r<R[0]):

>	eq11_11_3_:=T(r)=T[R[ext]]+(phi*r^2/k)*(1/r-1/R[ext]);eq11_11_3:=T[R[0]]=T[R[ext]]+(phi*R[0]^2/k)*(1/R[0]-1/R[ext]);

Fins. General 1D conduction with lateral sources:

>	eq11_12:=rho*A*dx*c*Diff(T,t)=k*(A+dA)*(Diff(T,x)+Diff(T,x,x)*dx)-k*A*Diff(T,x)+h*p*dx*(T[infinity]-T)+epsilon*sigma*p*dx*(T[infinity]^4-T^4)+phi*A*dx;

Fins, steady and with dA/dx=0 & no-sources: T(x), Q[root] and efficiencies:

>

eq11_13:=m=sqrt(h*p/(k*A));eq11_14:=diff(T(x),x,x)=m^2*(T(x)-T[infinity]);eq11_15:=(T(x)-T[infinity])/(T[0]-T[infinity])=cosh(m*(L-x))/cosh(m*L);eq11_16:=Q[root]=m*k*A*(T[0]-T[infinity])*tanh(m*L);eq11_16_1:=eta[T[0]]=Q[root]/(p*L*h*(T[0]-T[infinity]));eq11_16_2:=eta[T[0]]=tanh(m*L)/(m*L);eq11_16_3:=eta[Aroot]=Q[root]/(k*A*h*(T[0]-T[infinity]));eq11_16_4:=eta[Aroot]=(p*L/A)*tanh(m*L)/(m*L);

Definition of Biot and Fourier numbers:

>	eq11_17:=Bi=h*L/k;eq11_18:=Fo=a*t/L^2;

Heating/cooling of a perfect-conducting solid in a fluid (Bi=hL/k<<1, with L=V/A):

>	eq11_19:=rho*V*c*diff(T(t),t)=h*A*(T[infinity]-T);eq11_20:=(T(t)-T[infinity])/(T[0]-T[infinity])=exp(-Bi*Fo),Bi=h*V/(k*A),Fo=a*t*(A/V)^2;

Heat propagation in a semi-infinite solid subject to T-oscillations of period tau at the surface (t>>tau)

>	eq11_23:=T(x,t)=T[mean]+DT*exp(-x/sqrt(a*tau/Pi))*sin(2*Pi*t/tau-x/sqrt(a*tau/Pi));

Heat propagation in a semi-infinite solid subject to T-jump at the surface

>	eq11_23_1:=T(x,t)=T[0]-(T[0]-T[inf])*erf(x/sqrt(4*a*t));

Finite difference numerical simulation, 1D, centred. Full T(x,t) matrix. Valid for fins with h[lat] and/or e[lat]. Generic node.

>

eq11_24:=Dm*c*DT/Dt=Qnet;eq11_24_gen:=rho*A*Dx*c*(T[i,j+1]-T[i,j])/Dt=k*A*(T[i+1,j]-T[i,j])/Dx-k*A*(T[i,j]-T[i-1,j])/Dx+phi*A*Dx-p*Dx*(h[lat]*(T[i,j]-T[infinity])+epsilon[lat]*sigma*(T[i,j]^4-T[infinity]^4));eq11_24_gen__:=(T[i,j+1]-T[i,j])/Dt=a*(T[i+1,j]-2*T[i,j]+T[i-1,j])/Dx^2+phi/(rho*c)-(p/(rho*c*A))*(h[lat]*(T[i,j]-T[infinity])+epsilon[lat]*sigma*(T[i,j]^4-T[infinity]^4));eq11_24_gen_:=T[i,j+1]=T[i,j]+Fo*(T[i+1,j]-2*T[i,j]+T[i-1,j])+phi*Dt/(rho*c)-(p*Dt/(rho*c*A))*(h[lat]*(T[i,j]-T[infinity])+epsilon[lat]*sigma*(T[i,j]^4-T[infinity]^4));

Finite difference numerical simulation, 1D. Boundary nodes. You must adapt them to your particular problem. E=W/m2 absorbed.

>

eq11_24_0:=rho*A*(Dx/2)*c*(T[0,j+1]-T[0,j])/Dt=k*A*(T[1,j]-T[0,j])/Dx+phi*A*Dx/2-p*(Dx/2)*(h[lat]*(T[0,j]-T[infinity])+epsilon[lat]*sigma*(T[0,j]^4-T[infinity]^4))+A*(E0-h0*(T[0,j]-T0)-epsilon0*sigma*(T[0,j]^4-T0^4));eq11_24_0_:=T[0,j+1]=T[0,j]+2*Fo*(T[1,j]-T[0,j])+phi*Dt/(rho*c)-(p*Dt/(rho*c*A))*(h[lat]*(T[0,j]-T[infinity])+epsilon[lat]*sigma*(T[0,j]^4-T[infinity]^4))+(2*Dt/(rho*c*Dx))*(E0-h0*(T[0,j]-T0)-epsilon0*sigma*(T[0,j]^4-T0^4));eq11_24_N:=rho*A*(Dx/2)*c*(T[N,j+1]-T[N,j])/Dt=k*A*(T[N-1,j]-T[N,j])/Dx+phi*A*Dx/2-p*(Dx/2)*(h[lat]*(T[N,j]-T[infinity])+epsilon[lat]*sigma*(T[N,j]^4-T[infinity]^4))+A*(EN-hN*(T[N,j]-TN)-epsilonN*sigma*(T[N,j]^4-TN^4));eq11_24_N_:=T[N,j+1]=T[N,j]+2*Fo*(T[N-1,j]-T[N,j])+phi*Dt/(rho*c)-(p*Dt/(rho*c*A))*(h[lat]*(T[N,j]-T[infinity])+epsilon[lat]*sigma*(T[N,j]^4-T[infinity]^4))+(2*Dt/(rho*c*Dx))*(EN-hN*(T[N,j]-TN)-epsilonN*sigma*(T[N,j]^4-TN^4));;

Finite difference numerical simulation, 2D, centred, no sources. Only local T(x,y) matrix.

>	eq11_25:=(Tnew[i,j]-T[i,j])/Dt=a*(T[i+1,j]-2*T[i,j]+T[i-1,j])/Dx^2+a*(T[i,j+1]-2*T[i,j]+T[i,j-1])/Dy^2;eq11_25_:=Tnew[i,j]=T[i,j]+Fo*((T[i+1,j]-2*T[i,j]+T[i-1,j])+(Dy/Dx)^2*(T[i,j+1]-2*T[i,j]+T[i,j-1]));eq11_26:=Fo=a*Dt/Dx^2;eq11_27:=Fo*(1+(Dy/Dx)^2)<1/2;

Stefan problem (heat transfer through a semi-infinite phase-changing material) T[pc]=T[phase-change], DT=constant T-jump at the surface

>	eq11_28:=(T(x,t)-T[pc])/DT=erf(x/(2*sqrt(a*t)))/erf(sqrt(alpha))-1;eq11_29:=sqrt(Pi*alpha)*exp(alpha)*erf(alpha)=Ja;eq11_30:=x[pc]=2*sqrt(alpha*a*t);eq11_31:=Ja=c*DT/Dh[pc];

Mass diffusion balance

>	eq11_32:=Diff(rho[i],t)+Diff(rho[i]*v[i],x)=w[i];eq11_33:=Diff(rho,t)+Diff(rho*v,x)=0;

Fick's law (constitutive equation), mass flow & mass diffusion equation

>	eq11_34:=j[i]=-D[i]*Diff(rho[i],x);eq11_35:=j[i]=rho[i]*v[d,i];eq11_36:=Diff(rho[i],t)+Diff(rho[i]*v,x)=D[i]*Diff(rho[i],x,x)+w[i];

WARNING. A list of all variables follows, to copy and paste to the save command (after Maple7 there is no saving all). CAUTION: After pasting all, I must MANUALLY delete system variables: like RealRange_...

>	sort([anames()]):

>

save eq11_1, eq11_10_1, eq11_10_2, eq11_11_1,eq11_11_1_, eq11_11_2, eq11_11_2_, eq11_11_3, eq11_11_3_, eq11_12, eq11_13, eq11_14, eq11_15,eq11_16, eq11_16_1, eq11_16_2, eq11_16_3, eq11_16_4, eq11_17, eq11_18, eq11_19, eq11_1_0, eq11_1_1, eq11_1_2, eq11_2, eq11_20, eq11_23, eq11_23_1, eq11_24, eq11_24_gen, eq11_24_gen_, eq11_24_gen__, eq11_24_0, eq11_24_0_, eq11_24_N, eq11_24_N_, eq11_25, eq11_25_, eq11_26, eq11_27, eq11_28, eq11_29, eq11_2_0, eq11_2_1, eq11_2_2, eq11_3, eq11_30, eq11_31, eq11_32, eq11_33, eq11_34, eq11_35, eq11_36, eq11_4, eq11_4_1, eq11_4_2, eq11_5, eq11_5_1,eq11_5_2, eq11_5_3, eq11_5_4, eq11_5_5, eq11_5_6, eq11_6_10, eq11_6_11, eq11_6_20, eq11_6_21, eq11_6_22_polar, eq11_6_22_axial, eq11_6_30, eq11_6_31, eq11_7, eq11_7_1, eq11_7_2, eq11_7_3, eq11_8_1, eq11_8_2, eq11_9_1, eq11_9_2,   "../therm_eq11.m":

>