| > | restart:#"m09_p50" |
| > | read`../therm_eq.m`:read`../therm_chem.m`:with(therm_chem);with(therm_proc):with(plots): |
Considérese la fórmula empírica ponderal del carbón de madera como C7H4O. Se pide:
a) Fracción másica de carbono en ese carbón, y poder calorífico inferior (combustión del carbón de madera con aire), comparándolo con el del carbono.
b) Estequiometria y poder calorífico inferior en su reacción con nitrato de potasio (salitre) en proporción másica del 70 % de salitre y 30 % de carbón en polvo, sabiendo que solo se genera C, CO, H2O, N2 y K2CO3.
c) Para aproximar mejor la pólvora tradicional, considérese la mezcla de salitre, carbón y azufre de acuerdo a la estequiometria 4KNO3+C7H4O+S→2K2CO3+CO2+4CO+H2S+H2O+2N2. Determinar las fracciones másicas usadas, el poder calorífico inferior, y la cantidad de gases generados
d) En un cohete de feria se usan 10 g de esa pólvora para propulsar 250 g de carga. Determinar la velocidad de salida y la altura máxima alcanzable suponiendo que el rendimiento energético global es del 10 %.
Datos termoquímicos adicionales. KNO3(s): M=0,101 kg/mol, hf=494 kJ/mol, gf=394 kJ/mol, y s=133 J/(mol·K); K2CO3(s): hf=1150 kJ/mol, gf=1065 kJ/mol, y s=156 J/(mol·K); H2S(g): M=0,034 kg/mol, hf=21 kJ/mol, gf=33 kJ/mol, y s=206 J/(mol·K).
Datos:
| > | su0:="Aire":dat:=[Char=C7H4O,Sal=KNO3,Pot=K2CO3,ysal=0.7,Mchar=(7*12+4*1+16)*1e-3*kg_/mol_,Msal=(1*39+1*14+3*16)*1e-3*kg_/mol_,Msul=0.032*kg_/mol_,Mpot=(2*39+1*12+3*16)*1e-3*kg_/mol_,Msh2=(32+2*1)*1e-3*kg_/mol_,mp=0.01*kg_,mr=0.25*kg_,eta=0.1];dat:=op(subs(g=g0,[Const])),op(dat),SI2,SI1:hgssal:=-494e3*J_/mol_,-394e3*J_/mol_,133*J_/(mol_*K_);hgspot:=-1150e3*J_/mol_,-1065e3*J_/mol_,156*J_/(mol_*K_);hgssul:=0,0,32*J_/(mol_*K_);hgssh2:=-21e3*J_/mol_,-33e3*J_/mol_,206*J_/(mol_*K_);h[f,C7H4O]=0; |
a) Fracción másica de carbono en ese carbón, y poder calorífico inferior en su combustión con aire, comparándolo con el del carbono.
Para un compuesto CuHvOw, la fracción másica será yC:=u*M[C]/(u*M[C]+v*M[H]+w*M[O]).
El PC será el mismo que con oxígeno puro. Hemos de despreciar la entalpía de formación del compuesto C7H4O porque no es una molécula sino una fórmula ponderal.
| > | CuHvOw=C7H4O;yC:=u*M[C]/(u*M[C]+v*M[H]+w*M[O]);yC_:=evalf(7*12/(7*12+4*1+16));eqEST0:=eq_fit(7*C+2*H2+(1/2)*O2+c*O2=a*CO2+b*H2O);PCI_:=PCI(eqEST0);PCIm_:=subs(dat,%/Mchar);C+O2=CO2;PCI_C:=PCI(%);PCIm_C:=%/rhs(Mf("C")); |
| (1) |
i.e. C7H4O indica que tiene un 81 % de carbono en masa (más 4 % de hidrógeno y 15 % de oxígeno). Al arder en aire (aunque tiene algo de oxígeno necesita 7,5 moles adicionales de O2) genera 31 MJ por cada kilo de carbón vegetal (no conviene decir 3,2 MJ/mol porque la fórmula del fuel es ponderal, no molecular). Si fuera carbono puro generaría 33 MJ/kg.
b) Estequiometría y poder calorífico inferior en su reacción con nitrato de potasio (salitre) en proporción másica del 70 % de salitre y 30 % de carbón en polvo, sabiendo que solo se genera C, CO, H2O, N2 y K2CO3.
Sea xsal la fracción molar de salitre; la de carbón vegetal con la fórmula empírica dada será 1-xsal. Sea M la masa molar de la mezcla combustible/oxidante.
| > | eq7_5;xsal_:=subs(dat,(ysal/Msal)/(ysal/Msal+(1-ysal)/Mchar));eq7_2;M_:=subs(xsal=xsal_,dat,xsal*Msal+(1-xsal)*Mchar);eqEST1:=(1-xsal_)*C7H4O+xsal_*KNO3=a*C+b*CO+c*H2O+d*N2+e*K2CO3;BC:=(1-xsal_)*7=a+b+e;BH:=(1-xsal_)*4=2*c;BO:=(1-xsal_)*1+xsal_*3=b+c+3*e;BN:=xsal_*1=2*d;BK:=xsal_*1=2*e;sol_:=solve({BC,BH,BO,BN,BK},{a,b,c,d,e});eqEST1_:=subs(sol_,eqEST1);PCI_1mol:=b*h[f,CO]+c*h[f,H2O(g)]+e*h[f,K2CO3]-xsal*h[f,KNO3];PCI_1mol_:=-subs(sol_,dat,b*h7_+c*h6_+e*hgspot[1]-xsal_*hgssal[1]);PCI_1mass_:=PCI_1mol_/M_; |
![x[i] = `/`(`*`(y[i]), `*`(M[i], `*`(Sum(`/`(`*`(y[i]), `*`(M[i])), i = 1 .. C))))](images/p50_18.gif) |
|
![M = Sum(`*`(x[i], `*`(M[i])), i = 1 .. C)](images/p50_20.gif) |
|
| (2) |
i.e. la mezcla de 70 % en masa de salitre tiene un 71 % en base molar de salitre (y un 29 % de carbón vegetal para la fórmula dada), y se liberan 2,8 MJ por cada kg de mezcla.
Nota. Esta mezcla es una pólvora sin azufre usada como fulminante de otros explosivos; incluso se ha usado para extinción de fuegos porque al contacto con la llama (a unos 2000 K) el K2CO3 absorbe mucha energía al descomponerse en K2+CO2+(1/2)O2 (750 kJ/mol=5.5 MJ/kg). Una estequiometría sencilla muy usada para éstudiar estas pólvoras es 4 KNO3 + 5 C → 2 K2CO3 + 3 CO2 + 2 N2, que corresponde a 87 % de salitre y 13 % de carbono en masa. Si se quiere retener la composición ponderal del carbón como C7H4O, puede usarse 10 KNO3 + 2 C7H4O → 5 K2CO3 + 4 CO2 + 5 CO + 4 H2O + 5 N2, que corresponde a 83 % de salitre y 17 % de carbón vegetal en masa.
c) Para aproximar mejor la pólvora tradicional, considérese la mezcla de salitre, carbón y azufre de acuerdo a la estequiometría 4KNO3+3CH4O+2S→2K2CO3+2SO2+CO+4H2O+H2+2N2. Determinar las fracciones másicas usadas, el poder calorífico inferior, y la cantidad de gases generados
| > | eqEST2:=4*KNO3+C7H4O+S=2*K2CO3+CO2+4*CO+H2S+H2O+2*N2;ysal_:=4*Msal/(4*Msal+Mchar+1*Msul);ysal_:=subs(dat,%);ysul:=1*Msul/(4*Msal+Mchar+1*Msul);ysul_:=subs(dat,%);ychar_=1-ysal_-ysul_;;eq7_2;M:=(4*Msal+1*Mchar+1*Msul)/(4+1+1);M_:=subs(dat,%);PCI_2mol:=(h[f,CO2]+4*h[f,CO]+1*h[f,H2S(g)]+1*h[f,H2O(g)]+2*h[f,K2CO3]-4*h[f,KNO3]-h[f,C7H4O]-1*h[f,S])/(4+1+1);PCI_2mol_:=-subs(dat,(h4_+4*h7_+1*h6_+1*hgssh2[1]+2*hgspot[1]-4*hgssal[1])/(4+1+1));PCI_2mass_:=PCI_2mol_/M_;molGgenkg:=(molCO2+4*molCO+1*molH2S+1*molH2O+2*molN2)/(4*M_sal+M_char+1*M_sul);molGgenkg_:=subs(dat,(1+4+1+1+2)/(4*Msal+Mchar+1*Msul)); |
![M = Sum(`*`(x[i], `*`(M[i])), i = 1 .. C)](images/p50_39.gif) |
|
| (3) |
i.e. esta pólvora tiene 75 % en masa de salitre, más 19 % de carbón y 6 % de azufre), su masa molar media es de 90 g/mol, desprende 2,6 MJ/kg al reaccionar entre sí los componentes, y genera 16,7 molees gaseosos por cada kg de pólvora (16,7*22,4=374 L/kg a 0 ºC y 101 kPa).
Nota. Una de las estequiometrías más sencillas usadas para la pólvora es 2 KN03+3 C+S= K2S + 3 CO2 + N2, correspondiente a un 75 % en masa de salitre, 13 % de carbono, y 12 % de azufre. Con la fórmula ponderal del carbón vegetal dada se usa a veces 6 KNO3 + C7H4O + 2 S → 2 K2S + 4 CO2 + 3 CO + 2 H2O + 2 N2, correspondiente a un 78,3 % en masa de salitre, 13,4 % de carbón, y 8,3 % de azufre. La composición realmente usada para la pólvora tradicional desde mediados del siglo XIX es 75:15:10 en masa de salitre, carbón vegetal, y azufre.
d) En un cohete de feria se usan 10 g de esa pólvora para propulsar 250 g de carga. Determinar la velocidad de salida y la altura máxima alcanzable suponiendo que el rendimiento energético global es del 10 %.
Se entiende que el 10 % de la energía térmica liberada en la combustión pasa a energía potencial en el apogeo.
mp=masa de pólvora; mr=masa del cohete.
| > | eqeta:=eta=W/Q;eqeta:=eta=mr*g*h/(mp*PCI);eqPCI:=PCI=PCI_2mass_;z:=eta*mp*PCI/(mr*g);z_:=subs(PCI=PCI_2mass_,g=g0,dat,%); |
| (4) |
i.e. el cohete alcanzaría más de 1000 m de altura, lo que resulta excesivo. En realidad, estos cohetes apenas suben más de 100 m. La discrepancia es debida a que el rendimiento global del 10 % es exagerado. En primer lugar, al arder la pólvora, una parte de la energía química pasa a energía térmica del chorro de escape, y la otra parte se convierte en energía cinética del chorro (depende de la velocidad de salida de los gases, que puede rondar los 500 m/s). En segundo lugar, lo que produce el empuje es la cantidad de movimiento del chorro, que es la que se comunica al cohete, y no la energía del chorro; y este rendimiento propulsivo es muy pequeño en los cohetes. Y en tercer lugar, la resistencia aerodinámica será grande por las altas velocidades iniciales del cohete (que puede rondar los 30 m/s).
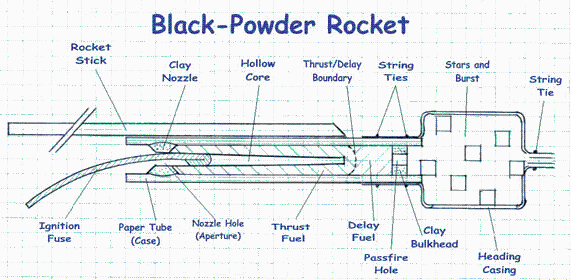
Detalle de un cohete de feria de tipo caña.
| > |