>	restart:#"m09_p38"

>	read`../therm_chem.m`:with(therm_chem);with(therm_proc):

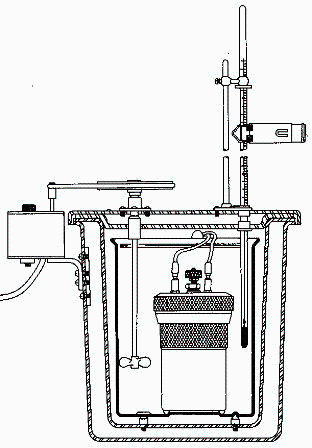
En una bomba calorimétrica de 0,3 L de capacidad se dispone una muestra de 1 g de glucosa (C6H12O6), se tapa, se inyecta lentamente oxígeno puro hasta una presión manométrica de 3 MPa, y se produce la ignición con una diminuta resistencia eléctrica. Sabiendo que el ambiente está a 25 ºC y 90 kPa, se pide:

a) Relación oxígeno/combustible usada, y comparación con la estequiométrica.

b) Poder calorífico másico (superior e inferior) del combustible usado.

c) Temperatura de combustión adiabática.

d) Temperatura que alcanzaría el cuerpo de la bomba, de 2,5 kg de acero inoxidable, si no hubiese agua exterior (i.e. si sólo se atemperaran adiabáticamente los gases con el cuerpo de la bomba).

Datos:

>	su1:="O2":su2:="N2":su3:="H2O":su4:="Acero_inox":fuel:=C6H12O6:dat:=[V=0.3e-3*m_^3,mf=1e-3*kg_,p1=3.09e6*Pa_,T1=(25+273.15)*K_,p0=90e3*Pa_,T0=(25+273.15)*K_,mB=2.5*kg_];

Eqs. const.:

>	dat:=op(dat),op(subs(g=g0,[Const])),SI2,SI1:Odat:=get_gas_data(su1):Ndat:=get_gas_data(su2):Wdat:=get_liq_data(su3):Bdat:=get_sol_data(su4):c_acero:=subs(%,c);Mf:=rhs(Mf(fuel));get_pv_data(su3):

a) Relación oxígeno/combustible usada, y comparación con la estequiométrica.

La cantidad de N2 que queda atrapada será muy pequeña, pero vamos a calcularla:

>	nN:=c79*p0*V/(R[u]*T0);nN_:=subs(dat,nN);mN:=nN*MN;mN_:=subs(Ndat,nN_*M)*1e3*g_/kg_;nO:=p1*V/(R[u]*T1);nO_:=subs(dat,nO);mO_:=subs(Odat,nO_*M)*1e3*g_/kg_;nf:='mf/Mf';nf_:=subs(dat,mf/Mf);Rox_f:='nO/nf';Rox_f_:=nO_/nf_;eqST:=eq_fit(fuel+a*O2=b*CO2+c*H2O);;Rox_fstq:=6;Rox_f_Rox_fstq:=Rox_f_/Rox_fstq;

i.e. hay 0,0086 mol de N2 (0,24 g) y se introducen 0,38 mol de O2 (12 g). La relación Oxi/Fuel es Rox_f=67 mol/mol, que es 11 veces la estequiométrica (Rox_fstq=6 mol/mol)

b) Poder calorífico másico (superior e inferior) del combustible usado.

Calcularemos los PC a p=cte aunque en este caso se realice la combustión a V=cte; la diferencia es siempre pequeña (PC_V=PC_p+Sum(nui)*Ru*T25) y aquí nula por ser Sum(nui)=6-6=0.

>	eq15_5;PCS_:=PCS(eqST);PCSm_:=PCS_/Mf;;PCI_:=PCI(eqST);PCIm_:=PCI_/Mf;;

i.e. el superior es 15,6 MJ/kg (2,8 MJmol), y el inferior 14,1 MJ/kg (2,54 MJ/mol).

c) Temperatura de combustión adiabática

>

eqTa_p:=eq15_7_2;eqMix_:=eqMIX(a*(fuel+Rox_f_*O2)=[2,4,5]);sol1_:=fsolve({eqNX,eqBC,eqBH,eqBO,eqBN},{a,x[Comp[2]],x[Comp[3]],x[Comp[4]],x[Comp[5]]});eqTa_p:=subs(sol1_,cpComp,dat,eq15_7_3);eqTa_V:=subs(c[p,i]=c[V,i],eq15_7_2);eqTa_V:=Ta=subs(cpComp,sol1_,Const,dat,T25+a*PCI_/(sum(delta[i]*x[Comp[i]]*(c[p,Comp[i]]-R[u]),i=1..C_)));

i.e. en la combustión (a V=cte) se alcanzarían 1520 K (algo menos porque se disociaría parte del CO2 a CO y O2, y por la transmisión de calor a las paredes durante el proceso). Luego se atemperaría con el entorno.

d) Temperatura que alcanzaría el cuerpo de la bomba, de 2,5 kg de acero inoxidable, si no hubiese agua exterior (i.e. si sólo se atemperaran adiabáticamente los gases con el cuerpo de la bomba).

Despreciando la capacidad térmica del interior, y dependiendo del agua que condense:

>	Q:=mf*PCSm;eqBE:=mB*cB*(TBf-T25)=Q;Q_:=subs(dat,mf*PCSm_);TBf_:=subs(cB=c_acero,dat,T25+Q_/(mB*cB));'TBf'=TKC(%);Q:=mf*PCIm;eqBE:=mB*cB*(TBf-T25)=Q;Q_:=subs(dat,mf*PCIm_);TBf_:=subs(cB=c_acero,dat,T25+Q_/(mB*cB));'TBf'=TKC(%);

i.e. el acero (y el interior) quedarías a 37 ºC si condensara toda el agua, o a 36 ºC si no condensara nada.

>	'nf'=nf_;'nO'=nO_;eqMIX(a*(nf_/mol_*fuel+nO_/mol_*O2)=[2,4,5]);sol_:=evalf(solve({eqBC,eqBH,eqBO,eqNX},{a,x[O2],x[CO2],x[H2O]}));eqSat:='x[H2O]=pv(T)/p1';Tdew_:=solve(subs(sol_,dat,x[H2O]=pv(T)/p1),T);'Tdew_'=TKC(%);

i.e. sí que condensa casi toda el agua (empezaría a condensar a 128 ºC), por lo que se llegaría a 37 ºC.

En la práctica el acero no está aislado sino en contacto con una masa de agua, que es donde se mide el calentamiento y de ahí se deduce el poder calorífico del combustible.

>