| > | restart:#"m09_p35" |
| > | read`../therm_chem.m`:with(therm_chem);with(therm_proc): |
Para determinar la capacidad térmica de una bomba calorimétrica, se quema una muestra de 1,230 g de ácido benzoico, C6H5COOH(s), con oxígeno puro a 3 MPa, 25 ºC y en cantidad triple de la estequiométrica, obteniéndose una subida de temperatura del baño de 4,33 ºC. Sabiendo que la entalpía de combustión estándar de esta sustancia patrón es de -3227 kJ/mol, se pide:
a) Entalpía de formación del ácido benzoico.
b) Masa de oxígeno consumido.
c) Calor transmitido.
d) Capacidad térmica de la bomba calorimétrica.
e) Estimar los valores máximos de temperatura y presión alcanzados en el proceso.
Datos:
| > | su:="O2":fuel:=C7H6O2:dat:=[mf=1.23e-3*kg_,p1=3e6*Pa_,T1=(25+273.15)*K_,lambda=3,DT=4.33*K_,hr25=-3227e3*J_/mol_,u=7,v=6,w=2,y=0]; |
Eqs. const.:
| > | dat:=op(dat),op(subs(g=g0,[Const])),get_gas_data(su),SI2,SI1: |
a) Entalpía de formación del ácido benzoico.
| > | eq1:=C7H6O2+(15/2)*O2=7*CO2+3*H2O;eq15_5;PC=-hr;eeqhr:=hr25=7*h4+3*h5-hf-(15/2)*h2;eeqhr:=subs(dat,hr25=7*h4_+3*h5_-hf-(15/2)*h2_);hf_:=solve(%,hf); |
![PC = `+`(`-`(Sum(`*`(nu[i], `*`(h[i])), i = 1 .. C)))](images/p35_4.gif) |
i.e. la entalpía de formación estándar del ácido benzoico sería de -385 kJ/mol (que coincide con el valores disponibles).
b) Masa de oxígeno consumido.
La estequiometría enseña que 1 mol de fuel requiere 7,5 mol de oxígeno, luego
| > | eqEst:=nO=nf*(15/2);nf=mf/Mf;Mf:=subs(dat,u*0.012+v*0.001+w*0.016)*kg_/mol_;nf_:=subs(dat,mf/Mf);eqEst_:=subs(nf=nf_,eqEst);mO_est:=nO*MO2;MO2:=subs(dat,M);mO_est_:=subs(eqEst_,mO_est);Vest:='mO_est*R*T25/p1';Vest_:=subs(dat,mO_est_*R*T25/p1);Vbomb:='lambda*Vest';Vbomb_:=subs(dat,lambda*Vest_); |
| (1) |
i.e. la combustión completa de 1,23 g de fuel (0,010 mol) requiere 2,42 g de oxígeno puro (0,076 mol de O2), que a 25 ºC y 3 MPa ocuparían 62 cm3.
Como hay el triple del estequiométrico, el volumen interno de la bomba calorimétrica será de 188 cm3 (más 1 cm3 o así, de los 1,23 g de combustible)
c) Calor transmitido.
Despreciando la variación de energía térmica de los productos atemperados respecto al estado estándar (i.e. suponiendo toda el agua líquida), el calor que sale es:
| > | eqBE:=Q=mf*PCSmV;eqBE:=Q=-nf*ur25;ur25:=hr25-(nCO2-nO2)*R[u]*T25;hr25_:=subs(dat,hr25);ur25_:=subs(Const,dat,hr25-(7-15/2)*R[u]*T25);Q_:=-nf_*ur25_; |
| (2) |
i.e. salen 32,5 kJ. Nótese que apenas hay diferencia entre la entalpía de reacción y la energía interna de reacción (i.e. entre el poder calorífico a presión constante y el de a volumen constante).
d) Capacidad térmica de la bomba calorimétrica.
| > | eqC:=Q=C*DT;C_:=subs(dat,Q_/DT);mw_eq:=C/c;mw_eq_:=C_/(4200*J_/(kg_*K_)); |
| (3) |
Esta es la capacidad térmica total, 7510 J/K, que incluye la del agua y la de los demás elementos del calorímetro (paredes de acero de la bomba, conectores, transductores, agitadores...), que en total equivale a 1,8 kg de agua.
e) Estimar los valores máximos de temperatura y presión alcanzados en el proceso.
La temperatura máxima será la de combustión adiabática a volumen constante.
El calor liberado, suponiendo que no hay disociaciones, con el agua en estado gaseoso es:
| > | eqBE:=Q='nf*PCI_V';PCI_V:=-u[r,v];PCI_V:=-h[r,v]+Dn*R[u]*T25;PCI_V:='-(7*h4_+3*h6_-hf_-(15/2)*h2_)+(7-15/2)*R[u]*T25';PCI_V:=subs(Const,dat,%);eqTa:=Ta='T25+nf*PCI_V/Sum(n[i]*c[v,i],i=1..C)';eqTa:=Ta='T25+nf*PCI_V/(nCO2*(c[p,CO2]-R[u])+nH2O*(c[p,H2O]-R[u])+nO2*(c[p,O2]-R[u]))';nO2left:=(lambda-1)*nO2est;nO2left_:=subs(dat,(lambda-1)*rhs(eqEst_));nH2O=3*nf;nH2O_:=3*nf_;nCO2=7*nf;nCO2_:=7*nf_;eqTa_:=subs(Const,nf=nf_,nCO2=nCO2_,nH2O=nH2O_,nO2=nO2left_,cpComp,dat,eqTa); |
![Ta = `+`(T25, `/`(`*`(nf, `*`(PCI_V)), `*`(Sum(`*`(n[i], `*`(c[v, i])), i = 1 .. C))))](images/p35_36.gif) |
|
| (4) |
i.e., unos 4070 K, muy alta para haber supuesto que no hay disociaciones. A esa temperatura la presión sería (también como límite superior):
| > | pmax:=n*R[u]*Ta/V;pmax:='(nCO2+nH2O+nO2)*R[u]*Ta/Vbomb_';pmax_:=subs(nCO2=nCO2_,nH2O=nH2O_,nO2=nO2left_,eqTa_,Const,dat,%); |
| (5) |
i.e. subiría de 3 MPa a 46 MPa (y luego bajaría en el atemperamiento).
Nótese que, tras el atemperamiento, la presión es menor que la inicial porque el H2O condensa:
| > | p2:='(nCO2+nO2)*R[u]*T25/Vbomb_';p2_:=subs(nCO2=nCO2_,nO2=nO2left_,Const,dat,%); |
| (6) |
i.e. cae de 3,0 MPa a 2,9 MPa.
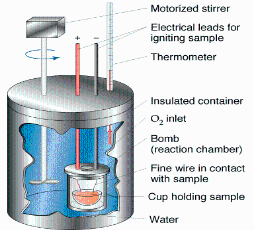
En la Fig. 1 se muestra un esquema rudimentario de este tipo de calorímetros.