>	restart:#"m09_34"

Dentro de un dispositivo cilindro-émbolo horizontal se han introducido en condiciones estándar 1 litro de dióxido de carbono y 4 litros más de hidrógeno. Considérese que, en presencia de un catalizador adecuado, los gases anteriores generan metano y agua. Se pide:
a) Determinar el volumen final atemperado, suponiendo reacción completa.
b) Determinar el calor y el trabajo que recibe o cede el sistema.
c) Plantear el sistema de ecuaciones que determinarían la composición en equilibrio químico a 1000 K y 1 MPa.

Datos:

>	read`../therm_chem.m`:with(therm_chem);with(therm_proc):

>	su1:="CO2":su2:="H2":su3:="CH4":su4:="H2O":dat:=[V1CO2=1e-3*m_^3,V1H2=4e-3*m_^3,Te=1000*K_,pe=1e6*Pa_];

Esquema:

>	datCO2:=get_gas_data(su1):datH2:=get_gas_data(su2):datCH4:=get_gas_data(su3):Wdat:=get_gas_data(su4),get_liq_data(su4):dat:=op(dat),op(subs(g=g0,[Const])),SI2,SI1:get_pv_data(su4):eq_esteq:=CO2+4*H2=CH4+2*H2O;eq_mezcla:=a*(CO2+4*H2)=x[CH4]*CH4+x[H2O]*H2O+x[CO2]*CO2+x[H2]*H2;

a) Determinar el volumen final atemperado, suponiendo reacción completa.

Inicialmente hay 1+4=5 litros de gases. Suponemos T1=25 ºC y p1=100 kPa.

Al reaccionar, si la reacción es completa, 1 mol de CO2 + 4 mol de H2 darían sólo un mol de gases (1 mol de CH4), puesto que prácticamente todo el agua quedaría condensada a T2=T1=25 ºC y p2=p1=100 kPa. Con el modelo de gas ideal, el volumen de gases es proporcional a la cantidad de sustancia, luego:

>	V:=n*R[u]*T/p;V2:=V1*n2/n1;V_:=subs(dat,(V1CO2+V1H2)*1/5);

i.e. los 5 litros iniciales se reducen al final a 1 litro. Si se hubiera tenido en cuenta el vapor disuelto en el gas, la cantidad en saturación sería (ley de Raoult) xv=p*(T2)/p2=0,03 (i.e. 0,03 mol de vapor en 1 mol de CH4), y por tanto el volumen no sería de 1 litro sino de 1,03 litros.

b) Determinar el calor y el trabajo que recibe o cede el sistema.

>	eq_esteq;[hr_std,gr_std,sr_std]=hgs_r25(%);n[CO2]=p1*V1CO2/(R[u]*T1);nCO2_:=subs(dat,p0*V1CO2/(R[u]*T25));Qsale=-hr_std*nCO2;Qsale_:=-hgs_r25(eq_esteq)[1]*nCO2_;Wmax_:=-hgs_r25(eq_esteq)[2]*nCO2_;

i.e. la entalpía de reacción es de -253 kJ por mol de CO2, indicando el signo menos que es una reacción exotérmica (salen 10 kJ de calor al ambiente).

La función de Gibbs de la reacción, -131 kJ/mol, indica que se podrían generar hasta 5,3 kJ (131 kJ/mol) en un dispositivo adecuado (e.g. tipo pila de combustible).

En el proceso descrito no se menciona que se haga trabajo sobre ningún otro sistema, así que, tras el atemperamiento (habiendo dejado que oscilase libremente el émbolo o habiéndolo fijado momentáneamente para evitar las enormes oscilaciones durante la combustión), como el sistema reduce su volumen de 5 litros a 1 litro, recibe un trabajo del ambiente:

>	W:=-p0*(V2-V1);W_:=subs(dat,-p0*(1/5-1)*(V1CO2+V1H2));

i.e. el sistema recibe 0,4 kJ del ambiente (en lugar de los 5,3 kJ que podría haber cedido si se hubiese aprovechado al máximo el proceso reactivo).

c) Plantear el sistema de ecuaciones que determinarían la composición en equilibrio químico a 1000 K y 1 MPa.

>	eq_mezcla:=eqMIX(a*(CO2+4*H2)=[10,5,4,8]);eqBC_:=eqBC;eqBH_:=eqBH;eqBO_:=eqBO;eqNX_:=eqNX;eqEQ_:=eqEQ(eq_esteq);eqEQ__:=evalf(subs(T=Te,p=pe,dat,eqEQ_));sol_:=fsolve({eqBC,eqBH,eqBO,eqNX,eqEQ__},{a,x[CH4],x[H2O],x[CO2],x[H2]},{x[H2]=0..1});

Nótese que, como enseña el Principio de Le Châtelier, al ser la reacción exotérmica, convendría establecer el equilibrio a baja temperatura para que diese mayor proporción de productos, y al reducirse la cantidad de sustancia en la reacción, convendría  establecer el equilibrio a alta presión.

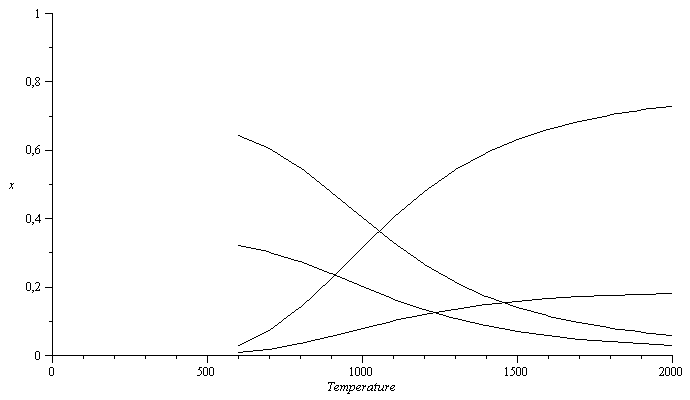
Variación de la composición con la T a p=1 MPa.

>

n:=15:arr:=array(1..n,1..5):for i from 1 to n do T:=evalf( 500+1500*(i/n))*K_;sol2:=fsolve(subs(p=pe,dat,{eqNX,eqBC,eqBH,eqBO,eqEQ_}),{a,x[CH4],x[H2O],x[CO2],x[H2]},x[H2]=0..1);arr[i,1]:=T/K_;arr[i,2]:=subs(sol2,x[CH4]);arr[i,3]:=subs(sol2,x[H2O]);arr[i,4]:=subs(sol2,x[CO2]);arr[i,5]:=subs(sol2,x[H2]);od:pl2:=pla(arr,2,1):pl3:=pla(arr,3,1):pl4:=pla(arr,4,1):pl5:=pla(arr,5,1):plot([pl2,pl3,pl4,pl5],Temperature=0..2000,x=0..1,color=black);

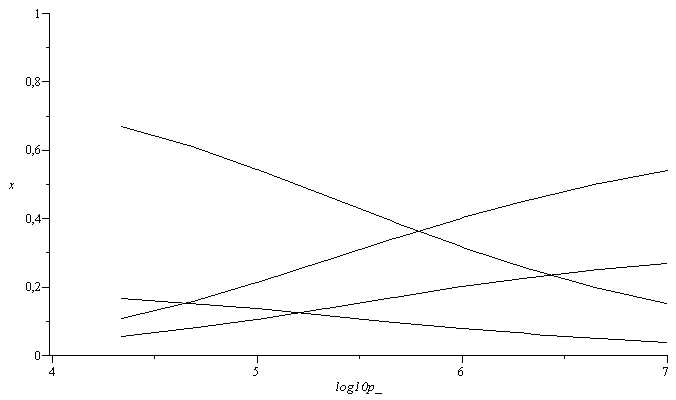
Variación de la composición con el log10 de p/Pa, a T=1000 K.

>

T:='T':n:=9:arr:=array(1..n,1..5):for i from 1 to n do log10p:=evalf( 4+3*(i/n));sol2:=fsolve(subs(T=Te,p=10^log10p*Pa_,dat,{eqNX,eqBC,eqBH,eqBO,eqEQ_}),{a,x[CH4],x[H2O],x[CO2],x[H2]},x[H2]=0..1);subs(T=Te,p=10^log10p*Pa_,[T,p]);arr[i,1]:=log10p;arr[i,2]:=subs(sol2,x[CH4]);arr[i,3]:=subs(sol2,x[H2O]);arr[i,4]:=subs(sol2,x[CO2]);arr[i,5]:=subs(sol2,x[H2]);od:pl2:=pla(arr,2,1):pl3:=pla(arr,3,1):pl4:=pla(arr,4,1):pl5:=pla(arr,5,1):plot([pl2,pl3,pl4,pl5],log10p_=4..7,x=0..1,color=black);

>