>	restart:#"m15_p29"

>	read`../therm_eq.m`:read`../therm_chem.m`:with(therm_chem);with(therm_proc):

En un proceso de producción de hidrógeno, se alimenta un reactor a presión ambiente con 0,1 kg/s de gas natural (supóngase metano) y un flujo molar triple del anterior de vapor de agua, entrando todo a 150 ºC y saliendo los productos a 800 ºC. Se pide:
a) Determinar la composición a la salida suponiendo que desaparece el metano y aparece monóxido de carbono.
b) Determinar el intercambio de energía con el exterior, en el caso anterior.
c) Determinar la composición a la salida suponiendo que desaparece el metano y aparece dióxido de carbono.
d) Determinar la composición a la salida suponiendo que aparecen ambos óxidos del carbono.

Datos:

>	su0:="Aire":su1:="CH4":su2:="H2O":su3:="H2":su4:="CO":dat:=[mGN=0.1*kg_/s_,b_a=3,T1=(150+273)*K_,p1=1e5*Pa_,T2=(800+273)*K_];

Eqs. const.:

>	dat:=op(subs(g=g0,[Const])),op(dat),SI2,SI1:Adat:=get_gas_data(su0):Fdat:=get_gas_data(su1):Wdat:=get_gas_data(su2),get_liq_data(su2):

a) Determinar la composición a la salida suponiendo que desaparece el metano y aparece monóxido de carbono.

Ante todo, determinemos el caudal de agua líquida necesario para el proceso.

>	nGN:=mGN/M;nGN_:=subs(Fdat,dat,nGN):'nGN'=evalf(%,2);nW:='b_a*nGN';nW_:=subs(dat,b_a*nGN_):'nW'=evalf(%,2);mW:='nW*M';mW_:=subs(Wdat,nW_*M):'mW'=evalf(%,2);VW:='mW*rho';VW_:=subs(Wdat,mW_/rho):'VW'=evalf(%,2);

>	eqMIX_:=eqMIX(a*(CH4+b_a*H2O)=[5,7,8]);eqBC;eqBH;eqBO;eqNX;sol1_:=solve(subs(dat,{eqBC,eqBH,eqBO,eqNX}),{a,x[H2O],x[CO],x[H2]}):evalf(%,2);eq1:=subs(sol1_,dat,eqMIX_/a);

b) Determinar el intercambio de energía con el exterior, en el caso anterior.

Balance energético en régimen estacionario (modelo de gases perfectos), sin trabajo y por unidad de cantidad de sustancia a la salida:

>

eqBE:=0=Wdot+Qdot+ndot[entry]*Sum(x[i]*h[t,i],i=1..C)-ndot[exit]*Sum(x[i]*h[t,i],i=1..C);eqBE:=0=q+a*PCI+(a*c[p,CH4]+a*b_a*c[p,H2O])*(T[entrada]-T25)-Sum(x[i]*c[p,i]*(T[salida]-T[std]),i=1..C);PCI_eq1_:=PCI(eq1):'PCI_eq1'=evalf(%,3);eqBE_:=subs(sol1_,cpComp,dat,0=q+a*PCI_eq1_+(a*c[p,CH4]+a*b_a*c[p,H2O])*(T1-T25)-(x[H2O]*c[p,H2O]+x[H2]*c[p,H2]+x[CO]*c[p,CO])*(T2-T25)):evalf(%,2);Qdot_:=subs(sol1_,dat,nGN_*solve(eqBE_,q)/a):'Qdot'=evalf(%,2);

i.e., la reacción sería endotérmica y se requiere aportar 2,2 MW (206 kJ/molCH4); normalmente, eso se consigue quemando más gas natural.

c) Determinar la composición a la salida suponiendo que desaparece el metano y aparece dióxido de carbono.

>

eqMIX_:=eqMIX(a*(CH4+b_a*H2O)=[4,5,8]);eqBC;eqBH;eqBO;eqNX;sol1_:=solve(subs(dat,{eqBC,eqBH,eqBO,eqNX}),{a,x[H2O],x[CO2],x[H2]}):evalf(%,2);eq1:=subs(sol1_,dat,eqMIX_/a);eqBE:=0=q+a*PCI+(a*c[p,CH4]+b_a*c[p,H2O])*(T[entrada]-T25)-Sum(x[i]*c[p,i]*(T[salida]-T[std]),i=1..C);PCI_eq1_:=PCI(eq1):'PCI_eq1'=evalf(%,3);eqBE_:=subs(sol1_,cpComp,dat,0=q+a*PCI_eq1_+(a*c[p,CH4]+b_a*c[p,H2O])*(T1-T25)-(x[H2O]*c[p,H2O]+x[H2]*c[p,H2]+x[CO2]*c[p,CO2])*(T2-T25)):evalf(%,2);Qdot_:=subs(sol1_,dat,nGN_*solve(eqBE_,q)/a):'Qdot'=evalf(%,2);

d) Determinar la composición a la salida suponiendo que aparecen ambos óxidos del carbono.

>

eqEQ_:=evalf(subs(T=T2,dat,eqEQ(CO2+H2=CO+H2O))):evalf(%,2);eqMIX_:=eqMIX(a*(CH4+b_a*H2O)=[4,5,7,8]);sol1_:=solve(subs(dat,{eqBC,eqBH,eqBO,eqNX,eqEQ_}),{a,x[H2O],x[CO],x[H2],x[CO2]}):evalf(%[1],2);eq1:=subs(sol1_,dat,eqMIX_/a);eqBE:=0=q+a*PCI+(a*c[p,CH4]+a*b_a*c[p,H2O])*(T[entrada]-T25)-Sum(x[i]*c[p,i]*(T[salida]-T[std]),i=1..C);PCI_eq1_:=PCI(eq1):'PCI_eq1'=evalf(%,3);eqBE_:=subs(sol1_,cpComp,dat,0=q+a*PCI_eq1_+(a*c[p,CH4]+a*b_a*c[p,H2O])*(T1-T25)-(x[H2O]*c[p,H2O]+x[H2]*c[p,H2]+x[CO2]*c[p,CO2]+x[CO]*c[p,CO])*(T2-T25)):evalf(%,2);Qdot_:=subs(sol1_,dat,nGN_*solve(eqBE_,q)/a):'Qdot'=evalf(%,2);

Se ve que el calor a aportar depende de la proporción de óxidos de carbono formados (2,2 MW si sólo sale CO, 1,5 MW si sólo sale CO2, y 2,2 MW si salen ambos en equilibrio (porque sale muy poco CO2).

Se podría estudiar la concentración de metano en equilibrio a la salida:

>	eqEQ2_:=evalf(subs(T=T2,p=p1,dat,eqEQ(CH4+H2O=CO+3*H2))):evalf(%,2);xCH4explicit_:=subs(sol1_,solve(eqEQ2_,x[CH4])):'xCH4explicit'=evalf(%,2);eqMIX_:=eqMIX(a*(CH4+b_a*H2O)=[4,5,7,8,10]);sol1_:=solve(subs(dat,{eqBC,eqBH,eqBO,eqNX,eqEQ_,eqEQ2_}),{a,x[H2O],x[CO],x[H2],x[CO2],x[CH4]}):evalf(%[1],2);

i.e., tanto si se resuelve explícitamente a partir de los resultados sin CH4, como si se hace exactamente, la concentración de CH4 en la salida es despreciable.

>

n:=19:arr:=array(1..n,1..7):for i from 1 to n do T[i]:=(400+1000*(i/n))*K_;eqEQ_:=evalf(subs(T=T[i],dat,eqEQ(CO2+H2=CO+H2O))):eqEQ2_:=evalf(subs(T=T[i],p=p1,dat,eqEQ(CH4+H2O=CO+3*H2))):sol1_:=fsolve(subs(dat,{eqBC,eqBH,eqBO,eqNX,eqEQ_,eqEQ2_}),{a,x[H2O],x[CO],x[H2],x[CO2],x[CH4]},{x[H2O]=0..1,x[CO]=0..1,x[H2]=0..1,x[CO2]=0..1,x[CH4]=0..1});arr[i,1]:=T[i]/K_;arr[i,2]:=subs(sol1_,x[Comp[4]]);arr[i,3]:=subs(sol1_,x[Comp[5]]);arr[i,4]:=subs(sol1_,x[Comp[7]]);arr[i,5]:=subs(sol1_,x[Comp[8]]);arr[i,6]:=subs(sol1_,x[Comp[10]]);od:pl2:=pla(arr,2,1):pl3:=pla(arr,3,1):pl4:=pla(arr,4,1):pl5:=pla(arr,5,1):pl6:=pla(arr,6,1):pl7:=pla(arr,7,1):plot([pl2,pl3,pl4,pl5,pl6,pl7],Temperature_K=0..1500,x=0..1,color=black);

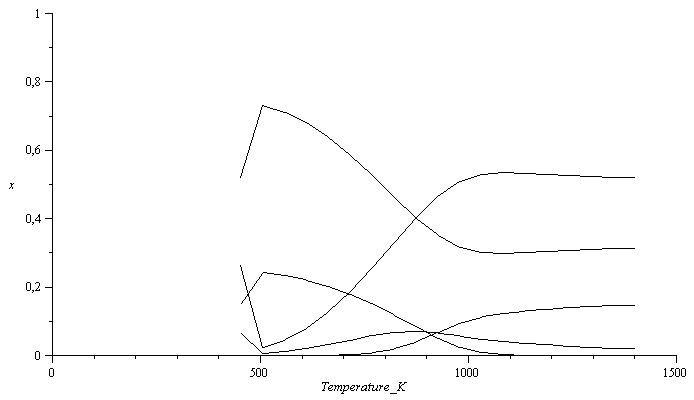Se ve claramente por qué es necesario trabajar a más de 1000 K.

>

;