>	restart:#"m09_p26"

En un tanque cerrado de 1 m3 conteniendo inicialmente aire en condiciones atmosféricas de 25 ºC y 100 kPa, se inyecta un poco de gasolina (aproxímese por n-octano). Se pide:
a) Indicar si habría peligro de explosión en el interior, en función de la cantidad inyectada.
b) Calcular la cantidad a inyectar para conseguir mezcla estequiométrica.
c) Representar esquemáticamente las variaciones de presión y temperatura en el interior en función del tiempo.
d) Calcular el poder calorífico de la gasolina inyectada (estequiométrica), e indicar lo que ocurriría si se produce la ignición.

Datos:

>	read`../therm_chem.m`:with(therm_chem):with(therm_proc):

>	fuel:=C8H18;fuel_:=convert(fuel,string):dat:=[V=1*m_^3,T1=(25+273)*K_];

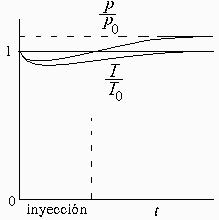
Esquema:

>

Eqs. const.:

>	Adat:=get_gas_data("Aire"):gdat:=get_gas_data(fuel_):ldat:=get_liq_data(fuel_):dat:=op(dat),op(subs(g=g0,[Const])),gdat,ldat,SI2,SI1:Mf(fuel);rho[fuel]:=subs(dat,rho);get_pv_data(fuel_):

a) Indicar si habría peligro de explosión en el interior, en función de la cantidad inyectada.

A 25 ºC y 100 kPa el n-octano (y la gasolina) está en estado líquido (Tb=399 K, Tabla A3.4).

Se sabe que la gasolina expuesta al aire se inflama al producir una chispa en la superficie (para temperaturas mayores de -40 ºC en la gasolina o mayores de 13 ºC en el n-octano), luego siempre que haya líquido al aire a 25 ºC habrá peligro de ignición por chispa.

Por otro lado, las mezclas gaseosas de n-octano y aire a 25 ºC y 100 kPa pueden inflamarse por una chispa sólo en el rango de concentraciones de combustible entre 1% y 6% de la mezcla (Tabla A3.9).

La inyección se supone que es rápida y pulverizada.

Se sabe que la gasolina es un líquido muy volátil, así que, incluso a 25 ºC, se evaporará rápidamente (sobre todo al estar finamente pulverizada).

Durante la inyección siempre habrá peligro de ignición en las proximidades del chorro.

Una vez mezclado y atemperado, sólo habrá peligro de ignición si la concentración de combustible está entre los límites de 1% y 6% de la mezcla (Tabla A3.9). Si hay menos del 1% de n-octano no hay peligro ninguno, pero si hay más del 6%, aunque no haya peligro en el interior, siempre habrá peligro en el exterior por escape de mezcla rica (y en el interior si entrara más aire).

b) Calcular la cantidad a inyectar para conseguir mezcla estequiométrica.

>

eq15_2;eqA0_molar:=evalf(Ateo(fuel),3);na:=p*V/(R[u]*T);na_:=subs(p=p0,T=T1,dat,na):'na'=evalf(%,2);nf:='na/A[0]';nf_:=na_/rhs(eqA0_molar):'nf'=evalf(%,2);mf:='nf*Mf';mf_:=nf_*rhs(Mf(fuel)):'mf'=evalf(%,2);Vf:='mf/rho[f]';Vf_:=mf_/rho[fuel]:'Vf'=evalf(%,2);xf:='nf/(nf+na)';xf_:=nf_/(nf_+na_):'xf'=evalf(%,2);

i.e. habría que inyectar 110 cm3 y se llegaría a una xf=0,017.

c) Representar esquemáticamente las variaciones de presión y temperatura en el interior en función del tiempo.

La presión puede bajar un poco al ir inyectando líquido, porque la evaporación genera moles pero disminuye la temperatura (dependerá de qué efecto sea mayor), aumentando luego hasta un valor final de (se supone que se evapora todo):

>	pf:='(na+nf)*R[u]*T/V';pf_:=subs(dat,(na_+nf_)*R[u]*T1/V):'pf'=evalf(%,3);

La temperatura disminuirá inicialmente por el enfriamiento evaporativo y luego se atemperará. Una estimación del valor máximo de este enfriamiento se obtendría del balance energético de la mezcla como masa de control, adiabática (Q=0) y a V=cte (W=0, en realidad W=-pDV=10^5*0,0001=11 J):

>	eqBE:=m[f]*h[lv,f]=m[a]*c[v]*DT;eqBE:=subs(dat,mf_*h[lv0])=subs(Adat,na_*M*c[v]*DT):evalf(%,2);DT_:=solve(%,DT):'DT'=evalf(%,2);

i.e. el aire se tendría que enfriar 29 ºC para vaporizar instantáneamente los 110 cm3 de n-octano, pero puede que la evaporación no sea tan rápida (dependerá de la atomización) y no sea bueno el modelo adiabático (entrará calor por las paredes).

Podría estimarse el tiempo que tardan en evaporarse las gotitas, con ayuda de la Ec. (11.35), tomando valores razonables para el radio de las gotitas (e.g. r=0,1 mm) y para la fracción másica de vapor saturado (e.g. Dy=0,1):

>	t[evap]:=(1/(2*Di*Dy))*(rho[l]/rho[a])*r^2;Di:=subs(rho=p0/(R*T0),Adat,dat,k/(rho*c[p])):'Di'=evalf(%,2);r=1e-4*m_;t[evap_]:=subs(rho[a]=1*kg_/m_^3,rho[l]=rho,r=1e-4*m_,Dy=0.1,dat,t[evap]):'t[evap]'=evalf(%,1);

Pues con esas suposiciones no parece descabellado el modelo adiabático, aunque al llegar las gotitas a la pared del recipiente éste contribuiría térmicamente a la evaporación. Nótese la decisiva importancia del tamaño de gota (gotas de 1 mm tardarían ya 200 s en evaporarse).

La experiencia parece indicar que toda la gasolina se evaporará más o menos rápidamente, pero puede calcularse cuanto n-octano haría falta introducir para que quedase en estado bifásico (saturado de vapor); con la teoría del aire húmedo:

>	x[sat]:=p[v,fuel,T]/p;eqAntoine:=p[v,fuel,T]=subs(dat,evalf(subs(dat,pv(T1)))):evalf(%,3);x[sat_]:=subs(dat,rhs(eqAntoine)/p0):'x[sat]'=evalf(%,2);

¡Qué sorpresa!, ¡casi estaría saturado!, ¡con lo volátil que es la gasolina!.

En realidad, la gasolina no es n-octano sino un destilado parcial del petróleo conteniendo una mezcla de hidrocarburos con una proporción apreciable de volátiles (e.g. de un 15% a un 30% de butanos: n-butano e i-butano) que hace que la xsat sea muchísimo mayor (mayor de xsat=0,5 a xsat=0,9).

Se concluye de aquí que el modelo de n-octano para la gasolina puede ser apropiado para estimar el poder calorífico, por ejemplo, pero no es válido para estimar la presión de vapor o la concentración en saturación.

d) Calcular el poder calorífico de la gasolina inyectada (estequiométrica) y lo que ocurriría si se produce la ignición.

>	eq1:=eq_fit(fuel+a*O2=b*CO2+c*H2O);PCS_:=PCS(eq1):'PCS'=evalf(%,2);PCSm_:=subs(dat,PCS_/rhs(Mf(fuel))):'PCSm'=evalf(%,2);nfPCS:='nf*PCS';nfPCS_:=nf_*PCS_:'nfPCS'=evalf(%,2);

El calor que desprendería la combustión del octano en condiciones estándar (a 100 kPa y 298 K y salida separada, i.e. agua líquida) sería de 3,7 MJ.

Si se produjese la ignición, la liberación brusca de tanta energía química aumentaría tanto la energía térmica (por ser rápido puede suponerse despreciable la transmisión de calor), que, al estar a volumen constante ocasionaría un incremento brusco de presión, normalmente superior al límite de rotura de los depósitos normales, y por tanto una explosión con proyección violenta hacia afuera de los fragmentos sólidos.

Una estimación del orden de magnitud del incremento de temperatura sería:

>	DT_p:='nfPCS/(na*cpa_molar)';DT_p_:=subs(Adat,dat,nfPCS_/(na_*M*c[p])):'DT'=evalf(%,1);

Esa estimación del DT=3000 K no es fina porque se ha hecho a p=cte y es a V=cte (la aumentaría), y se ha tomado el cp del aire frío (la disminuiría), pero puede servir para estimar el orden de magnitud del Dp: a V=cte, como n no varía mucho, Dp/p=DT/T=3000/300=10, i.e. la presión se multiplicaría por 10.

>