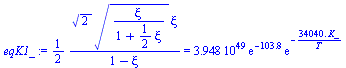En un dispositivo cilindro émbolo que mantiene la presión constante se tiene inicialmente 1 mol de CO2 a 25 °C y 100 kPa. Considérese el equilibrio CO2 = CO + (1/2)O2. Se pide:
a) Determinar la composición de equilibrio.
b) Calcular a qué temperatura la fracción molar de oxígeno es del 25%.
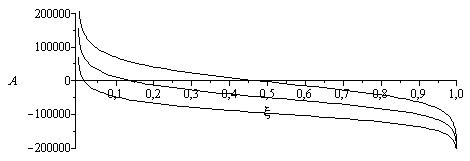
c) Representar la composición de equilibrio en función de la temperatura.
d) Representar el potencial de Gibbs en función del grado de avance de la reacción a 100 kPa y 2000 K, 2500 K y 3000 K, y determinar la composición de equilibrio.
Datos:
| > |
read`../therm_chem.m`:with(therm_chem):with(therm_proc): |
| > |
dat:=[T1=2000*K_,T2=2500*K_,T3=3000*K_,xO2=0.25,u=1,v=0,w=2,o=0,y=0]; |
Eqs. const.:
| > |
dat:=op(dat),op(subs(g=g0,[Const])),SI2,SI1: |
a) Determinar la composición de equilibrio.
Relación de mezcla:
| > |
eqMIX_:=eqMIX(a*CO2=[2,4,7]);eqMIXsol:=solve({eqNX,eqBC,eqBH,eqBO,eqBN},{a,x[Comp[4]],x[Comp[7]]});eqEST:=CO+(1/2)*O2=CO2;eqEQ_:=eqEQ(eqEST);eqEQ__:=subs(solve({eqBC,eqBO,eqNX},{x[CO2],x[CO],a}),eqEQ_);for i from 1 to 3 do eq2:=evalf(subs(T=T||i,p=p0,dat,eqEQ(eqEST)));sol1:=solve({op(eqMIXsol),eq2},{a,x[Comp[2]],x[Comp[4]],x[Comp[7]]}):print(T||i,evalf(sol1,2));od: |
b) Calcular a qué temperatura la fracción molar de oxígeno es del 25%.
| > |
eq2:=evalf(subs(p=p0,dat,eqEQ(eqEST))):'eq2'=evalf(%,2);sol1:=solve(subs(x[Comp[2]]=xO2,dat,dat,{op(eqMIXsol),eq2}),{a,T,x[Comp[4]],x[Comp[7]]}):'sol1'=evalf(%,2); |
c) Representar la composición de equilibrio en función de la temperatura.
| > |
n:=9:arr:=array(1..n,1..4):for i from 1 to n do T:=evalf( 500+4500*(i/n))*K_;eq2:=evalf(subs(p=p0,dat,eqEQ(eqEST))):sol2:=solve(subs(dat,dat,{op(eqMIXsol),eq2}),{a,x[Comp[2]],x[Comp[4]],x[Comp[7]]});arr[i,1]:=T/K_;arr[i,2]:=subs(sol2,x[Comp[2]]);arr[i,3]:=subs(sol2,x[Comp[4]]);arr[i,4]:=subs(sol2,x[Comp[7]])od:pl2:=pla(arr,2,1):pl3:=pla(arr,3,1):pl4:=pla(arr,4,1):plot([pl2,pl3,pl4],Temperature=0..5000,x=0..1,color=black); |
d) Representar el potencial de Gibbs en función del grado de avance de la reacción a 100 kPa y 2000 K, 2500 K y 3000 K, y determinar la composición de equilibrio.
| > |
for i from 1 to nops(Comp) do nu||i:=cat(nu,i):od:nu1_:=-1:nu2_:=1/2:nu3_:=1:n0:=[n01,n02,n03];n0_:=[1,0,0];n:=[seq(n0[i]+xi*nu||i,i=1..3)];n_:=[seq(n0_[i]+xi*nu||i||_,i=1..3)];i:='i':n_tot:=sum(n_[i],i=1..3);x:=[seq(n_[i]/n_tot,i=1..3)]; |
| > |
eq:=CO2=CO+(1/2)*O2;T:='T':hgsr:=hgs_r25(eq):hrR_:=hgsr[1]:'hrR'=evalf(%,2);grR_:=hgsr[2]:'grR'=evalf(%,2);eqK1:='Product((x[i]*(p/p0))^nu||i||_,i=1..3)=exp((-grR_+hrR_*(1-T25/T))/(R[u]*T25))';eqK1_:=(subs(dat,expand(subs(dat,subs(p=p0,Const,product('(x[i]*(p/p0))^nu||i||_',i=1..3)=exp((-grR_+hrR_*(1-T25/T))/(R[u]*T25))))))); |
| > |
i:='i':G:='sum(n[i]*mu[i],i=1..3)';mu[_]:=[seq(mu[R[i]]+R[u]*T*ln((x[i]*p/p0)),i=1..3)];i:='i':G:=subs(p=p0,sum(n_[i]*mu[_][i],i=1..3));G0:=eval(subs(xi=0,G));eq9_6:=A=-Sum(nu[i]*mu[i],i=1..C);eq_gr:=subs(A=R[u]*T*lnK,mu[i]=mu[R[i]],eq9_6);eq_gr:=expand(-R[u]*T*(-grR+hrR*(1-T25/T))/(R[u]*T25))=sum('nu||i||_*mu[R[i]]',i=1..3);eq_gr:=subs(grR=grR_,hrR=hrR_,Const,eq_gr):'eq_gr'=evalf(%,2); |
| > |
G_G0:=evalf(subs(Const,SI0,expand(subs(mu[R[1]]=solve(eq_gr,mu[R[1]]),G-G0)))):'G_G0'=evalf(%,2);plot({subs(T=2000+500*0,G_G0),subs(T=2000+500*1,G_G0),subs(T=2000+500*2,G_G0)},xi=1e-3..1,GG=-25000..25000,color=black); |
Puede comprobarse que los valores de G mínimos corresponden a los estados de equilibrio determinados anteriormente por el método de las constantes de equilibrio.
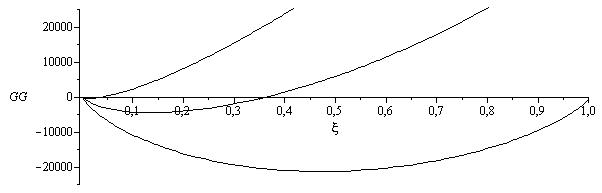
También se podrían haber calculado anulando la afinidad:
| > |
A:=-'Sum(nu[i]*mu[i],i=1..3)';nu:=[-1,1/2,1];A_:=evalf(subs(p=p0,Const,SI0,expand(subs(mu=mu[_],mu[R[1]]=solve(eq_gr,mu[R[1]]),A))));plot({subs(T=2000+500*0,A_),subs(T=2000+500*1,A_),subs(T=2000+500*2,A_)},xi=1e-3..1,'A'=-2e5..2e5,color=black); |
![`/`(`*`(x[CO2]), `*`(`^`(x[O2], `/`(1, 2)), `*`(x[CO]))) = `+`(`/`(`*`(0.2983e-4, `*`(exp(`+`(`/`(`*`(0.3404e5, `*`(K_)), `*`(T)))))), `*`(`^`(`/`(`*`(p0), `*`(p)), `/`(1, 2)))))](images/p06_5.gif)
![`+`(`/`(`*`(`/`(1, 2), `*`(`+`(1, `-`(`*`(3, `*`(x[O2])))))), `*`(`^`(x[O2], `/`(3, 2))))) = `+`(`/`(`*`(0.2983e-4, `*`(exp(`+`(`/`(`*`(0.3404e5, `*`(K_)), `*`(T)))))), `*`(`^`(`/`(`*`(p0), `*`(p)), `...](images/p06_6.gif)
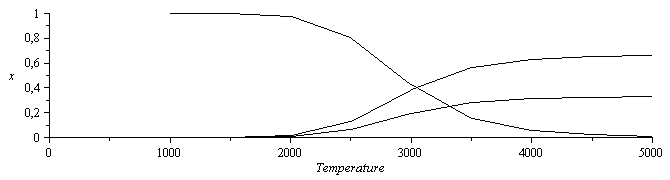
![Product(`^`(`/`(`*`(x[i], `*`(p)), `*`(p0)), nu || i || _), i = 1 .. 3) = exp(`/`(`*`(`+`(`-`(grR_), `*`(hrR_, `*`(`+`(1, `-`(`/`(`*`(T25), `*`(T)))))))), `*`(R[u], `*`(T25))))](images/p06_22.gif)