>	restart:#"m09_p02"

Se trata de estudiar de la 'reacción' de transformación del agua líquida en vapor, a partir de los datos de entalpía, función de Gibbs y entropía estándar. Se pide:

a) Determinar la temperatura de equilibrio a p atm.

b) Diferencia (analítica) entre hf(l) y hf(g).

c) Diferencia (analítica) entre gf(l) y gf(g).

d) Diferencia (analítica) entre s(l) y s(g).

e) Presión de vapor a 25 ºC.

Datos:

>	read`../therm_chem.m`:with(therm_chem):with(therm_proc):

>	su2:="H2O":

Eqs. const.:

>	Wdat:=get_gas_data(su2),get_liq_data(su2):get_pv_data(su2):dat:=op(subs(g=g0,[Const])),Wdat,SI2,SI1:

a) Determinar la temperatura de equilibrio de la 'reacción' de transformación del agua líquida en vapor, a partir de los datos de entalpía, función de Gibbs y entropía estándar.

>	H2O(l)=H2O(g);eq1:=eq9_10;eq2:=gr=grR+dgr_dT*(T-T25);eq3:=dg=-s*dT+v*dp;eq4:=dgr_dT=dg_dT_d||xi;eq2:=gr=grR-srR*(T-T25);

>	g25(g):=g6_:'g25(g)'=evalf(%,3);g25(l):=g5_:'g25(l)'=evalf(%,3);grR_:=g6_-g5_:'grR'=evalf(%,3);srR_:=s6_-s5_:'srR'=evalf(%,3);Teq_:=subs(grR=grR_,srR=srR_,gr=0,dat,solve(eq2,T)):'Teq'=evalf(%,3);

aprox. los 373 K de equil. liq-vap a p0. Se ve también que el proceso líquido-gas a 25 ºC y 100 kPa no es espontáneo pues tiene una gr=8,6 kJ/mol>0. También se podría ver que en esas condiciones es endotérmico (hr>0).

b) Diferencia (analítica) entre hf(l) y hf(g).

Será la Dh entre el estado real del H2O a (T25,p0) (liq) y el virtual de vapor a (T25,p0). Para ello, se puede pasar el líquido de (T25,p0) a (T25,pvT25) con el modelo de líquido perfecto (Dh=cDT+Drho/p), luego vaporizarlo,  y luego pasar virtualmente el gas de (T25,pvT25) a (T25,p0) con el modelo de gas perfecto (Dh=cpDT).

>	eq1:=h25(g)-h25(l)=(pvT25-p0)/rho+h[lv25]+0;h25(g)=h6_;h25(l)=h5_;pvT25_:=evalf(subs(Const,pv(T25)));h_[lv25]:=subs(Wdat,T=T25,dat,hlv(T));eq1_check:=h6_-h5_=subs(dat,((pvT25_-p0)/rho+h_[lv25]+0)*M);

que se aproxima bastante, pese al modelo

c) Diferencia (analítica) entre gf(l) y gf(g).

d) Diferencia (analítica) entre s(l) y s(g).

Empecemos por esta última, y procedamos igual: se pasa el líquido de (T25,p0) a (T25,pvT25) con el modelo de líquido perfecto (Ds=cln(T2/T1)), luego vaporizarlo,  y luego pasar virtualmente el gas de (T25,pvT25) a (T25,p0) con el modelo de gas perfecto (Ds=cp*ln(T2/T1)-Rln(p2/p1)).

>	eq3:=s25(g)-s25(l)=0+h[lv25]/T25-R*ln(p0/pvT25);s25(g)=s6_;s25(l)=s5_;eq3_check:=s6_-s5_=subs(dat,evalf(subs(dat,(0+h_[lv25]/T25-R*ln(p0/pvT25_))*M)));

aproximación aceptable. Nótese sin embargo, que, la aproximación s25(g)=s25(l)+hlv25/T25=70+44000/298=218 J/(mol·K) es bastante mala, ya que Ds=Dh/T es sólo válida en el equilibrio (Dg=0).

Y ahora volvamos a la función de Gibbs:

>	eq2:=g=h-T*s;eq2:=Dg25=Dh25-T25*Ds25;eq2:=g25(g)-g25(l)=h25(g)-h25(l)-T25*(s25(g)-s25(l));eq2_check:=g6_-g5_=h6_-h5_-subs(dat,T25)*(s6_-s5_);

aproximación aceptable.

Conclusión: si sólo se dispone de los valores termoquímicos del líquido (h5_,g5_,s5_), los del vapor ideal se podrían calcular como sigue:

>

eqDat:=[h25l,g25l,s25l]=[h5_,g5_,s5_];h25g:=h25l+hlv25+(pvT25-p0)/rho;h25g_:=rhs(eqDat)[1]+subs(dat,T=T25,dat,hlv(T)*M)+subs(dat,M*(pvT25_-p0)/rho);s25g:=s25l+hlv25/T25-R*ln(p0/pvT25)*M;s25g_:=rhs(eqDat)[3]+subs(dat,T=T25,dat,hlv(T)*M/T25)-subs(dat,evalf(subs(dat,M*R*ln(p0/pvT25_))));g25g:=g25l+'(h25g-h25l)-T25*(s25g-s25l)';g25g_:=rhs(eqDat)[2]+(h25g_-rhs(eqDat)[1])-subs(dat,T25)*(s25g_-rhs(eqDat)[3]);

que puede compararse con los datos tabulados:

>	eqDat:='[h25g,g25g,s25g]'=[h6_,g6_,s6_];

También es ilustrativa la representación de la función de Gibbs en función de la temperatura para el agua líquida y el agua vapor; el estado de equilibrio es el de menor g, que es el líquido para T<373 K y el vapor para T>373 K.

>	eqGL:=gL=gL25-sL25*(T-T25);eqGL_:=subs(gL25=g6_,sL25=s6_,cL=c,Wdat,dat,%):eqGV:=gV=gV25-sV25*(T-T25);eqGV_:=subs(gV25=g5_,sV25=s5_,cpV=c[p],Wdat,dat,%):plot(subs(T=T_K,SI0,[rhs(eqGL_),rhs(eqGV_)]/1000),T_K=298..400,g_kJ_mol=-250..-220);

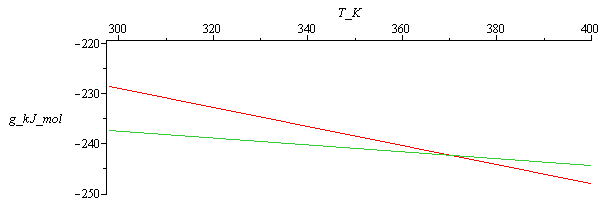que enseña que para T<Teq=373 K, a 100 kPa la fase natural es el líquido, y para T>Teq el vapor, como era de esperar.

e) Presión de vapor a 25 ºC.

Los valores termoquímicos tabulados pueden servir para calcular rápidamente la presión de vapor en condiciones estándar:

>	eqG_V_L:='g25g-g25l'=mu[V](T25,p0,1)-mu[L](T25,p0,1);eqG_V_L:='g25g-g25l'=mu[V](T25,pvT25,1)-M*R*T25*ln(pvT25/p0)-mu[L](T25,p0,1);eqG_V_L:='g25g-g25l'=-M*R*T25*ln(pvT25/p0);eqG_V_L_:=g6_-g5_=subs(dat,-M*R*T25*ln(pvT25/p0));pvT25_:=subs(dat,evalf(subs(dat,solve(%,pvT25))));

i.e. 3,12 kPa que coincide con el valor experimental (pv25=3.17 kPa).

>