>	restart:#"m08_p79"

Se mezclan adiabáticamente dos corrientes a 100 kPa, una de agua a Tw y gasto mw, y la otra de ma=1 kg/s de aire a 30 ºC y 60 % de HR. Se pide:
a) Humedad absoluta, y temperaturas de rocío y de bulbo húmedo a la entrada.
b) Relación de gastos másicos, mwa=mw/ma, para que, entrando el agua a 30 ºC, salga solo aire saturado.
c) Si entrara agua con un caudal mitad del valor anterior, determinar las condiciones de salida para Tw=5 ºC y para Tw=50 ºC, y representar en un diagrama psicrométrico el proceso que sigue el aire.
d) Si entrara agua con un caudal mil veces mayor del valor calculado en b), determinar las condiciones de salida para Tw=5 ºC y para Tw=50 ºC.
Datos:

>	read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):with(plots):interface(displayprecision=2):

>	su1:="Aire":su2:="H2O":dat:=[ma=1*kg_/s_,T0=(30+273)*K_,phi0=0.6,f1=1/2,Tw1=(5+273.15)*K_,Tw2=(50+273.15)*K_,f2=1000];

>	Adat:=get_gas_data(su1):Adat:=subs(c[p]=c[pa],R=R[a],M=M[a],T[b]=nada,[Adat]):Wgdat:=get_gas_data(su2):Wgdat:=subs(c[p]=c[pv],R=R[v],M=M[v],[Wgdat]):Wldat:=get_liq_data(su2):Wdat:=op(Wgdat),Wldat:get_pv_data(su2):dat:=op(dat),Const,SI2,SI1:

a) Humedad absoluta, y temperaturas de rocío y de bulbo húmedo a la entrada.

>

eq8_8;w0_:=evalf(subs(dat,w(phi0,T0,p0)));subs(T[R]=T[dew],eq8_9);pv0_:=subs(dat,evalf(subs(dat,pv(T0))));Tdew_:=evalf(subs(dat,solve(pv(T)=phi0*pv0_,T)));'Tdew_'=TKC(%);eq8_11;h0_:=subs(dat,Adat,Wdat,T=T0,dat,h(T,w0_));'h(Twet)=h0';Twet_:=(fsolve(subs(dat,Adat,Wdat,T=T0,dat,SI0,h(T,w(phi0,T,p0)))=subs(dat,Adat,Wdat,T=Twet,SI0,h(T,w(1,T,p0))),Twet=200..400))*K_;'Twet_'=TKC(%);

	(1)

i.e. el aire lleva w=16 g/kg de agua, y tiene Tdew=21,2 ºC, y Twet=23,6 ºC.

b) Relación de gastos másicos, mwa=mw/ma, para que, entrando el agua a 30 ºC, salga solo aire saturado.

Supondremos siempre que sale en equilibrio. Para que salga saturado a esa Twet hay que añadir un flujo de agua tal que:

>	w0wet_:=subs(dat,w(1,Twet_,p0));hwet_:=subs(dat,Adat,Wdat,T=Twet_,dat,h(T,w0wet_));mwa=mw/ma;mwa=w0wet-'w0';mwa_:=w0wet_-w0_;'1000*mva_'=%*1000;

	(2)

i.e. la relación ha de ser de mwa=2,6 g de agua por cada 1 kg de aire. Como era de esperar, el aire necesita poca agua para saturarse.

c) Si entrara agua con un caudal mitad del valor anterior, determinar las condiciones de salida para Tw=5 ºC y para Tw=50 ºC, y representar en un diagrama psicrométrico el proceso que sigue el aire.

Saldrá aire húmedo, no saturado, y casi con la misma entalpía de entrada (i.e. el proceso será prácticamente isoentálpico (ver gráfico final).

>

Tw_:=subs(dat,Tw1);hw_:=subs(Wdat,T=Tw1,dat,hl(T));h2=h0+mva*hw;h2_:=subs(dat,h0_+f1*mwa_*hw_);w=w0+mwa;w_:=subs(dat,w0_+mwa_*f1);eq8_11;T2_:=subs(dat,solve(h2_=subs(dat,Adat,Wdat,dat,h(T,w_)),T));'T2_'=TKC(%);Tw_:=subs(dat,Tw2);hw_:=subs(Wdat,T=Tw2,dat,hl(T));h2=h0+mva*hw;h2_:=subs(dat,h0_+f1*mwa_*hw_);w=w0+mwa;w_:=subs(dat,w0_+mwa_*f1);eq8_11;T2_:=subs(dat,solve(h2_=subs(dat,Adat,Wdat,dat,h(T,w_)),T));'T2_'=TKC(%);;

	(3)

efectivamente, el aire entra con h0=71,3 kG/kg y sale con h2=71,3 kJ/kg si el agua estaba a 5 ºC, o con h2=71,6 kJ/kg si estaba a 50 ºC, en ambos casos con una T2 de casi 27 ºC (26,7 ºC si el agua entra a 5 ºC, y 27,0 ºC si entra a 50 ºC).

d) Si entrara agua con un caudal mil veces mayor del valor calculado en b), determinar las condiciones de salida para Tw=5 ºC y para Tw=50 ºC.

Ahora saldrá una mezcla de agua líquida con aire saturado. Sea w3 el agua disuelta en el aire que sale, y mwa4=mw4/ma el resto.

>

eqBMw:=w0+mwa=w3+mwa4;eqBE:=h0+mwa*hw=h3+mwa4*h4;eqBM_:=subs(dat,w0_+f2*mwa_)=w3+mwa4;eqBE_:=subs(dat,h0_+f2*mwa_*subs(Wdat,T=Tw,hl(T)))=h3+mwa4*subs(Wdat,T=T3,hl(T));w3_:=subs(dat,w(1,T3,p0));h3_:=subs(Adat,Wdat,T=T3,h(T,w3_));Tw1=TKC(subs(dat,Tw1));sol1_:=fsolve(subs(Tw=Tw1,dat,SI0,subs(w3=w3_,h3=h3_,{eqBM_,eqBE_})),{T3,mwa4},{T3=273..373});T3w1_:=TKC(subs(sol1_,T3*K_));w3w1_:=evalf(subs(sol1_,SI0,w3_));Tw2=TKC(subs(dat,Tw2));sol2_:=fsolve(subs(Tw=Tw2,dat,SI0,subs(w3=w3_,h3=h3_,{eqBM_,eqBE_})),{T3,mwa4},{T3=273..373});T3w2_:=TKC(subs(sol2_,T3*K_));w3w2_:=evalf(subs(sol2_,SI0,w3_));

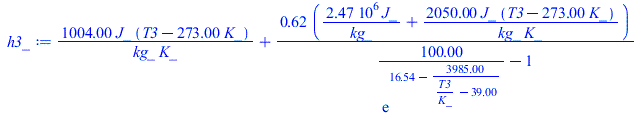	(4)

i.e. si entran 1 kg/s de aire a 30 ºC 60%HR (w0=16 g/kg) y 2,6 kg/s de agua a 5 ºC, salen 1 kg/s de aire a 9 ºC con w=7 g/kg en equilibrio con el agua, mientras que si entra el agua a 50 ºC sale todo a 41 ºC y el aire lleva 53 g/kg de agua disuelta.

>

pl:=plot(subs(dat,SI0,[[w(1,T,p0),T-273,T=273..323],[[w0_,T0-273],[w0wet_,Twet_-273]],[[w0_,T0-273],[w3w1_,subs(sol1_,T3-273)]],[[w0_,T0-273],[w3w2_,subs(sol2_,T3-273)]],[[0,Tw2-273],[1,Tw2-273]],[[0,Tw1-273],[1,Tw1-273]]]),w=0..0.08,T_C=0..51,color=black):pt:=textplot({[w0_,32,"entrada"],[w0wet_,23,"wet"],[w3w1_,9,"salida fría"],[w3w2_,41,"salida caliente"]}):display({pl,pt});

Conclusión:

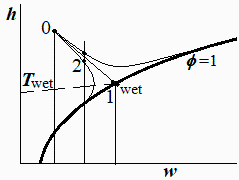
-Cuando entra muy poca agua (mw/ma<0,026), apenas cuenta su temperatura, y la salida está próxima a la reacta de h=h0=cte como se ha esquematizado en la primera figura.

-Cuando entra más agua de la de saturación adiabática (mw/ma>0,026), el aire a la salida está siempre en la curva de saturación (phi=1), acercándose a los extremos de temperatura del caudal de agua, pero no muy deprisa pues incluso con una relación mw/ma=1000·0,026=2,6 kg de agua por cada kg de aire, el aire solo se enfría hasta 9 ºC con agua a 5 ºC, o se calienta solo hasta 41 ºC con agua a 50 ºC, y la razón es que al enfriarse el aire húmedo condensa parte del agua que lleva disuelta, y al calentarse absorbe más y da lugar a un enfriamiento evaporativo (que en el caso frío sería un calentamiento 'condensativo'). Nótese que, aunque se han unido por líneas rectas el estado inicial y final, en realidad será un proceso de no equilibrio que se acerque mucho más al punto 'wet' antes de moverse a lo largo de la curva de saturación, como se indicó en la primera figura.

>