>	restart:#"m08_p72"

Se tiene una campana de vacío de 10 litros conteniendo inicialmente vapor de agua puro a 2 kPa y 25 ºC (estado 1), en presencia de aire ambiente a 100 kPa, 25 ºC, y 50 % de HR (estado 0). Sabiendo que a través de las juntas penetra lentamente aire ambiente al interior, se pide:

a) Humedad absoluta y relación molar de vapor respecto al aire seco ( ) en el aire ambiente, y cantidad de vapor inicialmente en el interior, nv1.

b) Considérese un estado genérico en el interior (estado 2) en el que ha entrado una cierta cantidad de aire ambiente, definida por su contenido de aire seco, na. Determinar la relación molar de mezcla,  (na), la relación másica de mezcla, w(na), y la presión, p(na), y sus valores para na=0.1 mol

c) Indicar cómo varía la humedad relativa en el interior.

d) Estado termodinámico en el equilibrio mecánico final (estado 3).

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):assume(m1ini>0,m1fin>0):

>	su1:="Aire":su2:="H2O":dat:=[V=10e-3*m_^3,p1=2e3*Pa_,T1=(25+273.15)*K_,p0=100e3*Pa_,T0=(25+273.15)*K_,phi0=0.5,na2=0.1*mol_];

Eqs. const.: 'v'=vapor, 'a'=aire seco.

>	dat:=op(dat),Const,SI2,SI1:Adat:=get_gas_data(su1):Adat:=subs(c[p]=c[pa],R=R[a],M=M[a],T[b]=nada,[Adat]):Wgdat:=get_gas_data(su2):Wgdat:=subs(c[p]=c[pv],R=R[v],M=M[v],[Wgdat]):Wldat:=get_liq_data(su2):Wdat:=op(Wgdat),Wldat:get_pv_data(su2):get_pv_data(su2):

a) Humedad absoluta y relación molar de vapor respecto al aire seco ( ) en el aire ambiente, y cantidad de vapor inicialmente en el interior, nv1.

wbar=nv/na; w=mv/ma; xv=nv/(na+nv);

>	eqET:=n=p*V/(R[u]*T0);wbar:=nv_na;wbar:=w/Mva;eq8_8;pv0_:=subs(dat,evalf(subs(dat,pv(T0))));w0_:=evalf(subs(dat,w(phi0,T0,p0)));wbar_:=subs(w=w0_,dat,wbar);nv1=p1*V/(R[u]*T1);nv1_:=subs(p=p1,dat,rhs(eqET));

	(1)

i.e. el estado 0 (aire ambiente) tiene una humedad absoluta de w=10 g/kg, y una wbar=0,016 (0.016 mol de 'v' por cada mol de 'a'), y en el interior (en el estado 1) hay 0,008 mol de 'v' (y nada de 'a').

b) Considérese un estado genérico en el interior (estado 2) en el que ha entrado una cierta cantidad de aire ambiente, definida por su contenido de aire seco, na. Determinar la relación molar de mezcla,  (na), la relación másica de mezcla, w(na), y la presión, p(na), y sus valores para na=0.1 mol

Si ha entrado na, también habrá entrado nv=na·wbar.

>

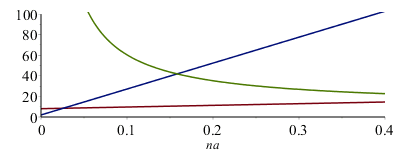
eqnv:=nvtot=nv1+nv;eqnv:=nvtot=nv1+na*'wbar';eqnv_:=nvtot=subs(SI0,nv1_+na*wbar_);eqp:=p=(nv1+nv+na)*R[u]*T0/V;eqp_:=subs(nv1=nv1_,nv=na*wbar_,dat,SI0,%);eqwbar:='wbar'=nv/na;eqwbar_:='wbar'=rhs(eqnv_)/na;eqw:=w=mv/ma;eqw:=w=Mva*nvtot/na;eqw_:=subs(eqnv_,dat,SI0,%);expand(%);plot(subs(eqnv_,eqp_,eqw_,[nvtot*1000,p/1000,w*1000]),na=0..0.4,0..100);wbar2:=subs(na=na2,dat,SI0,rhs(eqwbar_));w2:=subs(na=na2,dat,SI0,rhs(eqw_));'w2'=%*1000*g_/kg_;p2:=subs(na=na2,dat,SI0,rhs(eqp_))*kPa_/1000;

	(2)

En verde la humedad absoluta dentro w(na) en g/kg. Para na=0 tiende a infinito.

En azul p(na) en kPa, que va desde los 2 kPa iniciales hasta los 100 kPa finales.

En rojo, nv(na), i.e. la cantidad total de vapor dentro (en milimoles). Para na=0 vale nv=8 mmol.

Para na=0,1 mol, w=0,06 kg/kg, wbar=0,10 mol/mol, y p=27 kPa.

c) Indicar cómo varía la humedad relativa en el interior.

Al principio no tiene sentido hablar de humedad relativa, hasta que la presión interior no supere la de equilibrio líquido-vapor del agua pura a esa temperatura, pv0=3,2 kPa (e.g. a 25 ºC y 2,5 kPa, el aire que hubiera dentro admitiría, a esas p=cte y T=cte, una cantidad infinita de vapor sin llegar a condensar). Al ir aumentando la presión irá aumentando la humedad relativa, hasta que a una cierta presión y esos 25 ºC, llegue a saturarse.

>

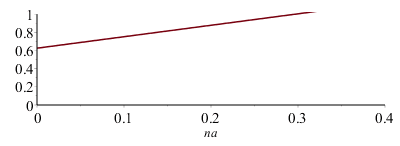
eqphi:=phi=x[v]/x[vsat];xvsat=p[v](T[0])/p;eqphi:=phi=(n[vtot]/(n[a]+n[vtot]))/(p[v](T[0])/p);eqphi_:=phi=subs(eqnv_,eqp_,dat,SI0,nvtot*p/((na+nvtot)*pv0_));expand(%);phi=asympt(rhs(%),na,3);plot(rhs(eqphi_),na=0..0.4,0..1);na_phi100:=solve(1=rhs(eqphi_),na)[2]*mol_;phi_na0:=subs(na=0,rhs(eqphi_));na_p_psat:=solve(pv0_/Pa_=rhs(eqp_),na)*mol_;phi_na0:=subs(na=0,rhs(eqphi_));phi_na_psat:=subs(na=na_p_psat/mol_,rhs(eqphi_));phi_na2:=subs(na=na2/mol_,dat,rhs(eqphi_));

	(3)

i.e. la HR empieza a estar definida para na=0,005 mol (con un valor phi=63 %), y va creciendo casi-linealmente con na (para na=0,1 mol vale phi=0,75) hasta la saturación (phi=1) para na=0,30 mol.

d) Estado termodinámico en el equilibrio mecánico final (estado 3).

Si no hubiéramos visto ya que se satura antes, obtendríamos para el estado 3 (p=p0=100 kPa):

>	p3:=p0;na3_:=solve(subs(dat,SI0,p0)=rhs(eqp_),na)*mol_;nv3_:=subs(na=na3_/mol_,rhs(eqnv_))*mol_;phi3_:=subs(na=na3_/mol_,rhs(eqphi_));

	(4)

pero no puede ser phi>1 en equilibrio; i.e. volvemos a ver que al final (estado 3) está sobresaturado, por lo que, en el equilibrio termodinámico (p=100 kPa, na=0,39 mol, nv=0,014 mol), el estado 3 sería bifásico, con una fase gaseosa saturada (phi=1) y gotitas dispersas, probablemente formadas sobre las paredes. Con phi=1 se puede calcular la cantidad de vapor en fase gaseosa, y el resto habría condensado.

>