>	krestart:#"m08_p70"

En una campana de vacío de de 8 litros hay inicialmente aire a 25 ºC, 94 kPa y 30% de HR. A partir de un cierto instante se hace funcionar una bomba de vacío volumétrica que aspira 1 L/s. Suponiendo que el proceso es suficientemente rápido, se pide:

a) Calcular la variación con el tiempo de la presión y la temperatura, y sus valores al cabo de 10 segundos.

b) Calcular la variación con el tiempo de la humedad relativa, determinando el instante en el que podría verse la condensación.

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):with(plots):

>	su1:="Aire":su2:="H2O":dat:=[Vc=8e-3*m_^3,p0=94e3*Pa_,T0=(25+273.15)*K_,phi0=0.3,Vp=1e-3*m_^3/s_,t1=10*s_];

Eqs. const.:

>	Adat:=get_gas_data(su1):Adat:=subs(c[p]=c[pa],R=R[a],M=M[a],T[b]=nada,[Adat]):Wgdat:=get_gas_data(su2):Wgdat:=subs(c[p]=c[pv],R=R[v],M=M[v],[Wgdat]):Wldat:=get_liq_data(su2):Wdat:=op(Wgdat),Wldat:get_pv_data(su2):dat:=op(dat),Const,SI2,SI1:

a) Calcular la variación con el tiempo de la presión y la temperatura, y sus valores al cabo de 10 segundos.

>	eqpS:=p=p0*(Vc/(Vc+Vp*t))^gamma;p_kPaS:=subs(Adat,dat,SI0,rhs(eqpS))/1000;eqTS:=T=T0*(Vc/(Vc+Vp*t))^(gamma-1);T_C:=subs(Adat,dat,SI0,rhs(eqTS))-273;eqpS10:=subs(t=t1,Adat,dat,eqpS);eqTS10:=subs(t=t1,Adat,dat,eqTS);T10_:=TKC(rhs(%));plot([p_kPaS,T_C],t=0..10,-50..100);

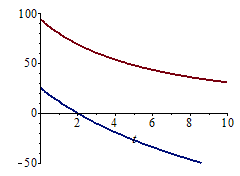i.e. al cabo de 10 s la presión interior (curva roja) sería de 30 kPa y la temperatura de -58 ºC (en verde). Sin embargo, no es plausible el modelo adiabático, y habría que considerar la entrada de calor desde las paredes por convección al aire residual (que todavía queda mucho, y el gradiente térmico es muy grande).

b) Calcular la variación con el tiempo de la humedad relativa, determinando el instante en el que podría verse la condensación.

>	eq8_8;w0_:=evalf(subs(dat,w(phi0,T0,p0)));pvT0:=subs(dat,evalf(subs(dat,pv(T0))));eq8_7;phi_percS:=subs(p=rhs(eqpS),Adat,dat,SI0,phi(w0_,T0*(p/p0)^((gamma-1)/gamma),p))*100;tsat:=fsolve(phi_percS=100,t=0..10)*s_;plot([p_kPaS,T_C,phi_percS],t=0..10,0..100);

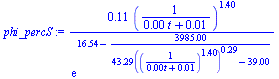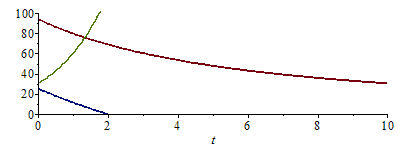i.e. en menos de 2 s (1,8 s) se debería ver la condensación (la HR es la curva verde, las otras son las de antes).

NOTA. Al realizar este experimento en el laboratorio no se ha observado visualmente la condensación (el interior permanece transparente), y todos los sensores de humedad disponibles tienen tiempos de respuesta mucho mayores y no sirven para medir en este proceso tan rápido. Sin embargo, cuando en vez de usar una bomba de vacío se usa una expansión brusca del aire encerrado desde una presión mayor a la presión ambiente, se ve claramente la condensación (cámara de niebla).

>