>	restart:#"m08_p69"

Se quiere comprimir 100 kg/s de aire ambiente en condiciones de 94 kPa, 30 ºC y 30% de HR, hasta 1 MPa usando compresores de rendimiento adiabático 0,85. Se pide:

a) Coste energético usando un compresor, y coste energético mínimo termomecánico.

b) Se piensa añadir agua pulverizada para conseguir el enfriamiento evaporativo del aire a la entrada. Determinar las temperaturas de rocío y de bulbo húmedo a la entrada, y la cantidad de agua necesaria para la humidificación adiabática hasta la saturación.

c) Comparar el coste energético de esta compresión (enfriada a la entrada) con la inicial.

d) Si en lugar del enfriamiento evaporativo a la entrada se usara una compresión escalonada con dos compresores y enfriamiento convectivo intermedio hasta la temperatura ambiente, usar el modelo de gas perfecto para plantear el consumo energético global en función de la presión intermedia y obtener el valor de ésta que lo hace mínimo (y este valor).

e) Si en lugar del enfriamiento convectivo intermedio se fueran a usar dos enfriamientos evaporativos hasta saturación, uno antes de cada compresor, calcular el agua necesaria y comparar el coste energético global con los anteriores.

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):with(plots):

>	su1:="Aire":su2:="H2O":dat:=[ma=100*kg_/s_,p0=94e3*Pa_,T0=(30+273.15)*K_,phi0=0.30,p1=1e6*Pa_,eta[C]=0.85];

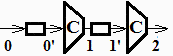
Eqs. const.:

>	Adat:=get_gas_data(su1):Adat:=subs(c[p]=c[pa],R=R[a],M=M[a],T[b]=nada,[Adat]):Wgdat:=get_gas_data(su2):Wgdat:=subs(c[p]=c[pv],R=R[v],M=M[v],[Wgdat]):Wldat:=get_liq_data(su2):Wdat:=op(Wgdat),Wldat:get_pv_data(su2):dat:=op(dat),Const,SI2,SI1:

a) Coste energético usando un compresor, y coste energético mínimo termomecánico.

Sin tener en cuenta los posibles cambios de composición (i.e. limitándonos al análisis termomecánico) y con el modelo de gas perfecto:

>

eq5_59;W_C:=m*c[p]*(T2-T1);W_C:=ma*c[pa]*T0*((p1/p0)^((gamma-1)/gamma)-1)/eta[C];W_C_:=subs(Adat,dat,%);T1_:=subs(T1=T0,p1=p0,p2=p1,Adat,dat,rhs(eq5_61));'T1_'=TKC(%);Wmin:=ma*(Dh-T0*Ds);Wmin:=ma*(c[p]*(T2-T1)-T0*(c[p]*ln(T2/T1)-R*ln(p2/p1)));Wmin:=ma*T0*R[a]*ln(p1/p0);Wmin_:=subs(dat,evalf(subs(Adat,dat,%)));

	(1)

i.e. el compresor consume 34.5 MW dejando el aire a 374 ºC (compresión adiabática con fricción) siendo el límite mínimo de 20.5 MW (compresión isoterma sin fricción).

b) Se piensa añadir agua pulverizada para conseguir el enfriamiento evaporativo del aire a la entrada. Determinar las temperaturas de rocío y de bulbo húmedo a la entrada, y la cantidad de agua necesaria para la humidificación adiabática hasta la saturación.

>

eqTdew0:=phi[0]*p[v](T[0])=p[v](T[dew]);Tdew0_:=solve(subs(dat,SI0,phi0*pv(T0)=pv(T)),T)*K_;'Tdew0_'=TKC(%);eq8_10;Twet0_:=(solve(subs(dat,Adat,Wdat,T=T0,dat,SI0,h(T,w(phi0,T,p0)))=subs(dat,Adat,Wdat,SI0,h(T,w(1,T,p0))),T))*K_;'Twet0_'=TKC(%);eq8_8;pvT0:=subs(dat,evalf(subs(dat,pv(T0))));w0_:=evalf(subs(dat,w(phi0,T0,p0)));%*1e3*g/kg;wwet0_:=subs(dat,w(1,Twet0_,p0));%*1e3*g/kg;mw0sa:=ma*(wwet0-w0);mw0sa_:=subs(dat,ma*(wwet0_-w0_));

	(2)

i.e. la temperatura de rocío del aire ambiente es 10,5 ºC, la de bulbo húmedo 17,5 ºC, y habría que añadir 0,51 kg/s de agua para que el aire ambiente entrase al compresor saturado.

c) Comparar el coste energético de esta compresión (enfriada a la entrada) con la inicial.

Seguimos usando las propiedades del aire seco (cp,gamma) para el aire húmedo, pues no llega ni al 2% la influencia del vapor disuelto.

>	W_Ce:=(ma+mw)*c[p]*(T2e-Twet0);W_Ce:=(ma+mw)*c[pa]*Twet0*((p1/p0)^((gamma-1)/gamma)-1)/eta[C];W_Ce_:=subs(mw=mw0sa_,Twet0=Twet0_,Adat,dat,%);T1e_:=subs(T1=Twet0_,p1=p0,p2=p1,Adat,dat,rhs(eq5_61));'T1e_'=TKC(%);

	(3)

i.e. con el enfriamiento evaporativo a la entrada el coste baja desde 34,5 MW a 33,3 MW (y en vez de 100 kg/s tendremos 100,5 kg/s de aire comprimido). La salida quedaría a 347 ºC en vez de 374 ºC.

d) Si en lugar del enfriamiento evaporativo a la entrada se usara una compresión escalonada con dos compresores y enfriamiento convectivo intermedio hasta la temperatura ambiente, usar el modelo de gas perfecto para plantear el consumo energético global en función de la presión intermedia y obtener el valor de ésta que lo hace mínimo (y este valor).

>

wC1y2:=c[p]*T0*((pin/p0)^((gamma-1)/gamma)-1)/eta[C]+c[p]*T0*((p1/pin)^((gamma-1)/gamma)-1)/eta[C];dw_dpin:=diff(%,pin)=0;pio:=solve(%,pin):pio:=sqrt(p0*p1);pio_:=subs(dat,SI0,%)*Pa_;WC:=ma*c[pa]*T0*((p1/p0)^((gamma-1)/gamma)-1)/eta[C];WC_:=subs(Adat,dat,%);WC1y2_:=subs(c[p]=c[pa],Adat,pin=pio_,dat,ma*wC1y2);T1i_:=subs(T1=T0,p1=p0,p2=pio_,Adat,dat,rhs(eq5_61));'T1i_'=TKC(%);

	(4)

i.e. la presión intermedia óptima es 307 kPa, y el ahorro es del 16% (28.8 MW en vez de 34,5 MW). El aire sale dell primer compresor a 173 ºC.

Para ver si el modelo de gas perfecto es apropiado, hay que comprobar que no condensa vapor a alta presión al enfriar.

>	eq8_7;p_T_w_:=subs(dat,[pio_,T0,w0_]);phi_:=evalf(subs(dat,phi(w0_,T0,pio_)));#Tmin_phi_1:=fsolve(1=evalf(subs(dat,SI0,phi(w0_,T,pio_))),T)*K_;'Tmin_phi_1'=TKC(%);

	(5)

Pues sí, no llega a condensar (pero casi). En la práctica habría que contar con un salto mínimo de 5 ºC o 10 ºC para que el tamaño del cambiador de calor fuese razonable.

e) Si en lugar del enfriamiento convectivo intermedio se fueran a usar dos enfriamientos evaporativos hasta saturación, uno antes de cada compresor, calcular el agua necesaria y comparar el coste energético global con los anteriores.

El proceso de saturación del aire ambiente antes del primer compresor ya se hizo antes.

El primer compresor (manteniendo la misma presión intermedia):

Entrada: p0=94 kPa, Twet0=17,5 ºC, wwet0=13,7 g/kg.

Salida: pio=307 kPa, T1ie1, wwet0=13.7 g/kg.

>	T1ie1_:=subs(T1=Twet0_,p1=p0,p2=pio_,Adat,dat,rhs(eq5_61));'T1ie1_'=TKC(%);phi1i_:=subs(dat,phi(wwet0_,T1ie1_,pio_));

	(6)

Proceso de saturación del aire ambiente después del primer compresor (saturación adiabática a p=cte):

>	eq8_10;Twet1_:=(solve(subs(dat,Adat,Wdat,T=T1ie1_,dat,SI0,h(T,w(phi1i_,T,pio_)))=subs(dat,Adat,Wdat,SI0,h(T,w(1,T,pio_))),T))*K_;'Twet1_'=TKC(%);wwet1e2_:=subs(dat,w(1,Twet1_,pio_));%*1e3*g/kg;mw1sa:='ma*(wwet1e2_-wwet0_)';mw1sa_:=subs(dat,%);

	(7)

i.e. la corriente sale del primer compresor a 307 kPa, 155 ºC y HR=1,2% (w=wet0=13.7 g/kg), y al saturarla adiabáticamente se enfría hasta 63 ºC, pasando de llevar 13.7 g/kg a llevar 50 g/kg de agua disuelta.

El consumo de los compresores sería:

>	WC1:=(ma+'mw0sa_')*c[pa]*Twet0*(('pio_'/p0)^((gamma-1)/gamma)-1)/eta[C];WC1_:=subs(Twet0=Twet0_,Adat,dat,%);WC2:=(ma+'mw0sa_+mw1sa_')*c[pa]*Twet1*((p1/'pio_')^((gamma-1)/gamma)-1)/eta[C];WC2_:=subs(Twet1=Twet1_,Adat,dat,%);W12:=WC1_+WC2_;

	(8)

i.e. con un sólo compresor se necesitaban 34,5 MW; con dos compresores con enfriamiento convectivo intermedio 28,8 MW; con dos compresores con enfriamiento evaporativo a la entrada de ambos se necesitarían 30,5 MW, pero en este caso se obtendrían casi 104 kg/s de aire comprimido en vez de 100 kg/s (para obtener 100 kg/s sólo se consumirían 29,3 MW), y nos evitaríamos el enorme cambiador de calor (y la caída de presión correspondiente).

>