>	restart:#"m08_p67"

Considérese el proceso de mezcla adiabática de una corriente de 1 m3/s de aire ambiente a 30 ºC, 90 kPa y 50% de HR, y un flujo de agua líquida mw a temperatura Tw. Suponiendo que se alcanza el equilibrio, se pide:

a) Temperaturas de rocío a la entrada, y gasto másico de aire seco.

b) Temperaturas de bulbo húmedo y humedad absoluta a la entrada, y humedad absoluta correspondiente al proceso ideal de saturación adiabática en esas condiciones.

c) Calcular el estado tras el proceso de mezcla, para el caso mw=10 kg/s y Tw=5 ºC (como primera aproximación, puede suponerse que la temperatura de salida es la de entrada del agua).

d) Calcular el estado tras el proceso de mezcla, para el caso mw=10 kg/s y Tw=95 ºC.

Datos:

>	read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):

>	su1:="Aire":su2:="H2O":dat:=[Vdot=1*m_^3/s_,T0=(30+273)*K_,p0=90e3*Pa_,phi0=0.5,mwin=10*kg_/s_,Twin1=(5+273.15)*K_,Twin2=(95+273.15)*K_];

>	Adat:=get_gas_data(su1):Adat:=subs(c[p]=c[pa],R=R[a],M=M[a],T[b]=nada,[Adat]):Wgdat:=get_gas_data(su2):Wgdat:=subs(c[p]=c[pv],R=R[v],M=M[v],[Wgdat]):Wldat:=get_liq_data(su2):Wdat:=op(Wgdat),Wldat:get_pv_data(su2):dat:=op(dat),Const,SI2,SI1:

a) Temperaturas de rocío a la entrada, y gasto másico de aire seco.

Es de esperar que resulte Tdew unos grados por debajo de T0, y ma aproximadamente 1 kg/s.

>	eq8_9;Tdew:=evalf(solve(subs(dat,pv(T)=phi0*pv(T0)),T));'Tdew'=TKC(%);eqm:=mdot=rho*Vdot;eq8_12;eq8_8;w0_:=evalf(subs(dat,w(phi0,T0,p0)));rho_:=subs(w=w0_,p=p0,T=T0,Adat,dat,rhs(eq8_12));eqm_:=subs(rho=rho_,dat,eqm);eqma:=ma=mdot/(1+w0);eqma_:=subs(eqm_,w0=w0_,eqma);

i.e. TRocío=18,3 ºC y ma=1.01 kg/s, aunque dentro del nivel de incertidumbre asumido se puede aproximar por ma=p*Vdot/(Ra*T)=1.02 kg/s e incluso ma=1 kg/s como se preveía.

b) Temperaturas de bulbo húmedo y humedad absoluta a la entrada, y humedad absoluta correspondiente al proceso ideal de saturación adiabática.

La Twet estará entre Tdew y T0, y la w0 será del orden del 1%.

>	eq8_10;h0_:=subs(dat,Adat,Wdat,T=T0,dat,h(T,w0_));Tsa_:=(fsolve(subs(dat,Adat,Wdat,T=T0,dat,SI0,h(T,w(phi0,T,p0)))=subs(dat,Adat,Wdat,T=Tsa,SI0,h(T,w(1,T,p0))),Tsa=200..400))*K_;'Tsa_'=TKC(%);'w0'=w0_;w0sa:=subs(dat,w(1,Tsa_,p0));

i.e. Twet=21,5 ºC, w0=15 g/kg y w0sa=18,5 g/kg.

c) Calcular el estado tras el proceso de mezcla, para el caso mw=10 kg/s y Tw=5 ºC (como primera aproximación, puede suponerse que la temperatura de salida es la de entrada del agua).

Con tanta agua, saldrá una mezcla bifásica con aire saturado y agua (suponemos que el aire disuelto es despreciable). Supoiendo que la mezcla sale a la temperatura de entrada del agua (Tw):

>	eqS:=T1=Twin;subs(Twin=Twin1,dat,%);w1_:=evalf(subs(dat,SI0,w(1,Twin1,p0)));eqBMw:=mw+ma*w0=mw1+ma*w1;eqBMw_:=mw1='mwin+ma*(w0-w1)';mw1_:=subs(eqma_,w0=w0_,w1=w1_,dat,rhs(%));

i.e., parte del vapor disuelto en el aire condensa (el aire entra con 15 g/kg y sale con 6,2 g/kg).

Ahora se puede estimar mejor la temperatura de salida, T1 (que será algo mayor) con el balance energético:

>	eqBE:=mwin*cw*(Twin-T[tr])+ma*h0=mw1*cw*(T1-T[tr])+ma*h1(T1,w1);h1_:=subs(Adat,Wdat,T=T1,dat,h(T,w1_));eqBE_:=subs(eqma_,h0=h0_,h1=h1_,w1=w1_,Adat,Wdat,dat,T=T1,mw1_*c*(Twin1-T[tr])+ma*h0=mw1_*c*(T1-T[tr])+ma*h(T,w1_));T1_:=subs(dat,solve(%,T1));'T1'=TKC(%);

i.e. en lugar de a 5 ºC, la mezcla sale a 6 ºC (no hay que iterar porque el efecto sobre w1 será despreciable).

Nótese que la fracción gaseosa media en una sección es alta; con igual velocidad de ambas fases, sus áreas de paso respectivas estarán en la relación de caudales: 1 m3/s de aire y 10/1000=0,01 m3/s de agua; i.e. la fase líquida ocuparía un 1% de la sección recta del conducto. En la práctica las velocidades no serán iguales porque en tubería horizontal el flujo de agua sería anular concentrado en la parte baja y más lento, y en tubería vertical la gravedad modificaría grandemente el flujo de agua.

d) Calcular el estado tras el proceso de mezcla, para el caso mw=10 kg/s y Tw=95 ºC.

En general, hay 3 incógnitas:

  T1=temperatura de la mezcla a la salida.

  mw1=flujo de agua líquida a la salida.

  w1=humedad absoluta de la fase gaseosa a la salida.

>	eqBMw:=mwin+ma*w0=mw1+ma*w1;eqBE:=mwin*cw*(Twin-T[tr])+ma*h0=mw1*cw*(T1-T[tr])+ma*h1(T1,w1);w1='w(1,T1,p0)';

>

w1_:=subs(dat,SI0,w(1,T1,p0));h1_:=subs(Adat,Wdat,SI0,T=T1,h(T,w1_));eqBE_:=subs(eqma_,h0=h0_,w1=w1_,Adat,Wdat,dat,SI0,T=T1,mwin*c*(Twin2-T[tr])+ma*h0=mw1*c*(T1-T[tr])+ma*h(T,w1_));eqBMw_:=subs(eqma_,w0=w0_,w1=w1_,dat,SI0,eqBMw);sol_:=fsolve({eqBE_,eqBMw_},{T1,mw1},{T1=273..373}):T1_:=subs(sol_,T1)*K_;'T1_'=TKC(%);mw1_:=subs(sol_,mw1)*kg_/s_;'w1_'=evalf(subs(T1=T1_/K_,w1_));

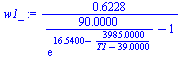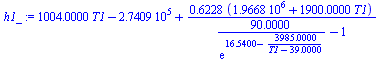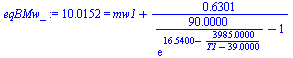i.e., como se evapora un poco de agua (el aire pasa de llevar 15 g/kg a llevar 394 g/kg de vapor disuelto), la temperatura del agua baja apreciablemente (de los 95 ºC de entrada a los 73 ºC de salida)..

>

ADICIONAL. Podemos estudiar la influencia de la temperatura de entrada del agua, Twin:

>

print("Twin       T1        mw1       w1");for i from 0 to 9 by 3 do Tw:=5+10*i+273.15;w1_:=subs(dat,SI0,w(1,T1,p0));h1_:=subs(Adat,Wdat,SI0,T=T1,h(T,w1_));eqBE_:=subs(eqma_,h0=h0_,w1=w1_,Adat,Wdat,dat,SI0,T=T1,mwin*c*(Tw-T[tr])+ma*h0=mw1*c*(T1-T[tr])+ma*h(T,w1_));eqBMw_:=subs(eqma_,w0=w0_,w1=w1_,dat,SI0,eqBMw);sol_:=fsolve({eqBE_,eqBMw_},{T1,mw1},{T1=273..373}):T1_:=subs(sol_,T1)*K_;'T1_'=TKC(%);mw1_:=subs(sol_,mw1)*kg_/s_;print(TKC(Tw*K_),TKC(T1_),mw1_,evalf(subs(T1=T1_/K_,w1_)));od:

i.e. al mezclar 1 kg/s de aire a 30 ºC con 10 kg/s de agua a Tw=(5..95) ºC, la mezcla sale a T1=(6..73) ºC, saturada, con w1=(7..394) g/kg en la fase gaseosa.

Nótese que si el agua entra muy fría, en lugar de evaporarse se condensa y sale más líquido del que entra.

¿Y para un gasto de agua pequeño?

>

mwin:=0.01*kg_/s_;print(" Tw       T1        mw1          w1");for i from 0 to 9 by 3 do Tw:=5+10*i+273.15;w1_:=subs(dat,SI0,w(1,T1,p0));h1_:=subs(Adat,Wdat,SI0,T=T1,h(T,w1_));eqBE_:=subs(eqma_,h0=h0_,w1=w1_,Adat,Wdat,dat,SI0,T=T1,mwin*c*(Tw-T[tr])+ma*h0=mw1*c*(T1-T[tr])+ma*h(T,w1_));eqBMw_:=subs(eqma_,w0=w0_,w1=w1_,dat,SI0,eqBMw);sol_:=fsolve({eqBE_,eqBMw_},{T1,mw1},{T1=273..373}):T1_:=subs(sol_,T1)*K_;'T1_'=TKC(%);mw1_:=subs(sol_,mw1)*kg_/s_;print(TKC(Tw*K_),TKC(T1_),mw1_,evalf(subs(T1=T1_/K_,w1_)));od:

i.e. si mw << ma, la temperatura del agua de aporte influye poco, saliendo la mezcla cerca de la Tsa=21,5 ºC antes calculada.

Obviamente, si mw >> ma, las condiciones de entrada del aire casi no influirían (incluso podría disolverse el aire en el agua y salir una sola fase).

La solubilidad del aire en agua a 95 ºC y 90 kPa es del orden de 1 mg/kg (a 0 ºC y 100 kPa es 30 mg/kg para el N2 y 70 mg/kg para el O2, pero disminuye mucho con la temperatura, tendiendo a cero en ebullición), por lo que sólo se disolverían 0,01 kg/s de los 1,01 kg/s de aire de entrada.

>

Agua que hace falta para saturar el aire (que depende poco de la T0).

>	eqBMw:=mw+ma*w0=ma*w1;eqBMw:=mw+ma*w0=ma*w0sa;mwsa:='ma*(w0sa-w0)';mwsa_:=subs(eqma_,w0=w0_,w0sa=w0sa_,%);

i.e. bastan 3,5 g/s de agua para saturar la corriente de aire.

>