>	restart:#"m08_p53"

Para el acondicionamiento ambiental de un local, se toma aire de la atmósfera, que está a 35 ºC y 30%HR, y se produce aire a 15 ºC y 70%HR mediante el enfriamiento de una fracción del aire aspirado (condensando parte del agua) y la mezcla posterior con la otra fracción. Se pide:
a) Determinar la temperatura de rocío, la entalpía y la humedad absoluta del aire de entrada.
b) Determinar la temperatura de rocío, la entalpía y la humedad absoluta del aire de salida.
c) Plantear las ecuaciones del mezclado de ambas fracciones, indicando las incógnitas.
d) Resolver el problema anterior.
e) Determinar la fracción másica condensada.
f) Representación del proceso en el diagrama h-w.

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):

>	su1:="Aire":su2:="H2O":dat:=[T0=(35+273)*K_,phi0=0.3,T3=(15+273)*K_,phi3=0.7];

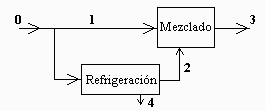
Esquema:

>

>

Eqs. const.:

>	Adat:=get_gas_data(su1):Adat:=subs(c[p]=c[pa],R=R[a],M=M[a],T[b]=nada,[Adat]):Wgdat:=get_gas_data(su2):Wgdat:=subs(c[p]=c[pv],R=R[v],M=M[v],[Wgdat]):Wldat:=get_liq_data(su2):Wdat:=op(Wgdat),Wldat:get_pv_data(su2):dat:=op(dat),Const,SI2,SI1:

a) Determinar la temperatura de rocío, la entalpía y la humedad absoluta del aire de entrada.

Supondremos proceso isobárico a p=100 kPa.

>	eq8_9;phi0=subs(dat,phi0);pv0_:=subs(dat,evalf(subs(dat,pv(T0)))):p[v](T0)=evalf(%,2);TR0_:=subs(dat,evalf(subs(dat,solve(pv(T)=phi0*pv(T0),T)))):T[R]=evalf(%,3);eq8_8;w0_:=subs(dat,evalf(subs(dat,w(phi0,T0,p0)))):'w0'=evalf(%,2);h=h(T,w);h0_:=subs(Adat,Wdat,T=T0,dat,h(T,w0_)):h0=evalf(%,2);

i.e. Trocio=15 ºC, h0=62 kJ/kg y w0=11 g/kg.

b) Determinar la temperatura de rocío, la entalpía y la humedad absoluta del aire de salida.

>	phi3=subs(dat,phi3);pv3_:=subs(dat,evalf(subs(dat,pv(T3)))):p[v](T3)=evalf(%,2);TR3_:=subs(dat,evalf(subs(dat,solve(pv(T)=phi3*pv(T3),T)))):T[R]=evalf(%,3);w3_:=subs(dat,evalf(subs(dat,w(phi3,T3,p0)))):'w3'=evalf(%,2);h=h(T,w);h3_:=subs(Adat,Wdat,T=T3,dat,h(T,w3_)):h3=evalf(%,2);

c) Plantear las ecuaciones del mezclado de ambas fracciones, indicando las incógnitas.

Sea lambda la fracción de aire derivada al refrigerador. Dividimos todo por el gasto de aire seco de entrada, ma.

>	eqBMa:="(1-lambda)+lambda"=1;eqBMw:=(1-lambda)*w1+lambda*w2=w3;w1:=w0;eqBE:=(1-lambda)*h1+lambda*h2=h3;h2=h(T,w2);h1:=h0;eq8_8;phi2:=1;

Queda un sistema de 2 ecuaciones (eqBMw,eqBE) con dos incógnitas (lambda,T2), una vez substituidas w2(phi2,T2) y h2(T2,w2).

d) Resolver el problema anterior.

>

w2_:=subs(dat,w(phi2,T2,p0)):'w2'=evalf(%,2);h2_:=subs(Adat,Wdat,T=T2,dat,h(T,w2_)):'h2'=evalf(%,2);eqBE_:=subs(h0=h0_,h2=h2_,h3=h3_,w2=w2_,dat,eqBE):'eqBE'=evalf(%,2);eqBMw_:=subs(w0=w0_,w2=w2_,w3=w3_,dat,eqBMw):'eqBMw'=evalf(%,2);sol1_:=fsolve(subs(SI0,{eqBMw_,eqBE_}),{T2,lambda},T2=200..400):T2_:=subs(sol1_,T2)*K_:'T2'=evalf(%,3);lambda_:=subs(sol1_,lambda):'lambda'=evalf(%,2);h2__:=subs(dat,evalf(subs(T2=T2_,h2_))):'h2'=evalf(%,2);w2__:=evalf(subs(T2=T2_,w2_)):'w2'=evalf(%,2);

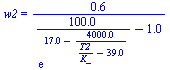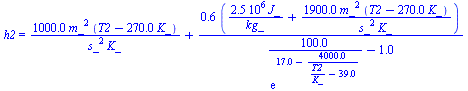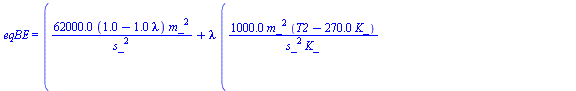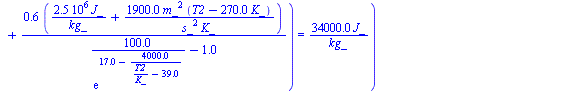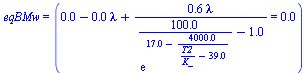i.e. hay que refrigerar hasta 7 ºC el 71% del gasto de aire.

e) Determinar la fracción másica condensada.

>	eqBMw02:=mw_cond=ma*(w0-w2);eqBMw02:=mw_cond/ma=w0-w2;eqBMw02:=mw_cond/ma=w0_-w2__:evalf(%,2);

i.e. condensan 4,4 g de agua por kg de aire de entrada.

f) Representación del proceso en el diagrama h-w.

Aproximando por T-w:

>	plot(subs(dat,SI0,[[w(1,T,p0),T-273,T=273..313],[[w0_,T0-273],[w0_,TR0_-273]],[[w3_,T3-273],[w3_,TR3_-273]],[[w0_,T0-273],[w2__,T2_-273]]]),w=0..0.02,T=0..40,color=black);

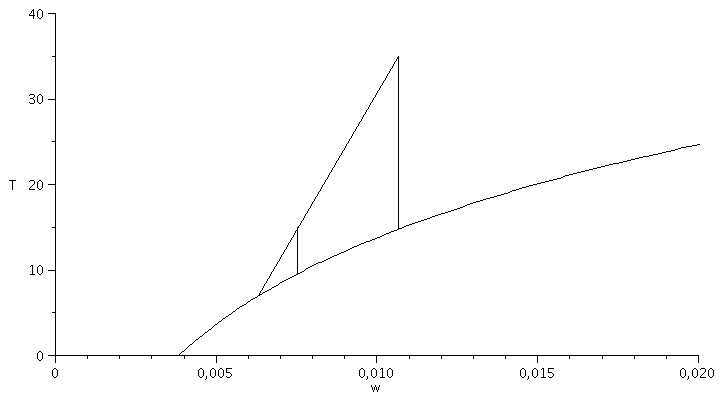Nótese que la resolución gráfica resulta trivial: basta prolongar la recta que une los puntos 0 y 3 hasta cortar a la de saturación en el diagrama h-w (no en el T-w, pero casi).