| > | restart:#"m08_p52" |
Se ha llenado lentamente una botella de plástico (PET) de 1,5 L y 0,2 mm de espesor con aire a 105 kPa, a partir de aire ambiente a 25 ºC, 95 kPa y 65% de humedad relativa. Tras una maniobra rápida de una llave de paso, la presión interior baja bruscamente hasta 100 kPa. Se pide:
a) Determinar la humedad absoluta y relativa del aire encerrado inicialmente.
b) Determinar la temperatura interior y la humedad relativa en el interior tras el escape.
c) Determinar si con una descarga rápida hasta la presión ambiente se llegaría a empañar la botella.
d) Determinar la presión de llenado a la que empezaría a empañarse la botella en el llenado lento.
Datos:
| > | read"../therm_eq.m":read"../therm_proc.m":with(therm_proc): |
| > | su1:="Aire":su2:="H2O":dat:=[p1=105e3*Pa_,T0=(25+273)*K_,p0=95e3*Pa_,phi0=0.65,p2=100e3*Pa_]; |
Esquema:
| > |
| > |
Eqs. const.:
| > | Adat:=get_gas_data(su1):Adat:=subs(c[p]=c[pa],R=R[a],M=M[a],T[b]=nada,[Adat]):Wgdat:=get_gas_data(su2):Wgdat:=subs(c[p]=c[pv],R=R[v],M=M[v],[Wgdat]):Wldat:=get_liq_data(su2):Wdat:=op(Wgdat),Wldat:get_pv_data(su2):dat:=op(dat),Const,SI2,SI1: |
a) Determinar la humedad absoluta y relativa del aire encerrado inicialmente.
| > | eq8_8;w0_:=subs(dat,evalf(subs(dat,w(phi0,T0,p0)))):'w0'=evalf(%,2);T1:=T0;w1:=w0;eq8_4;eq8_7;phi1_:=evalf(subs(dat,phi(w0_,T1,p1))):'phi1'=evalf(%,2); |
i.e. si no se ha perdido agua durante el llenado (e.g. se ha echo a mano despacio, y no a partir de aire seco de un compresor industrial), la humedad absoluta no varía, pero la humedad relativa aumenta proporcionalmente a la presión.
b) Determinar la temperatura interior y la humedad relativa en el interior tras el escape, suponiendo modelo de gas perfecto no condensable.
La evolución será isoentrópica. Si empezamos suponiendo que no condensa:
| > | T1:=T0;T2:=T1*(p2/p1)^((gamma-1)/gamma);T2_:=subs(Adat,dat,T2):'T2'=evalf(%,3);'T2'=evalf(T2_/K_-273,4)*`ºC`;w2:=w1;phi2_:=evalf(subs(dat,phi(w0_,T2_,p2))):'phi2'=evalf(%,2); |
i.e. el aire interior quedaría a 21 ºC y 88%HR.
c) Determinar si con una descarga rápida hasta la presión ambiente se llegaría a empañar la botella.
| > | p3:=p0;T3:=T1*(p3/p1)^((gamma-1)/gamma);T3_:=subs(Adat,dat,T3):'T3'=evalf(%,3);'T3'=evalf(T3_/K_-273,4)*`ºC`;w3:=w1;phi3_:=evalf(subs(dat,phi(w0_,T3_,p3))):'phi3'=evalf(%,2); |
phi3>1, luego sí condensaría y empañaría la pared interior.
d) Determinar la presión de llenado a la que empezaría a empañarse la botella en el llenado lento.
En la compresión isoterma phi/p=cte.
| > | p4:=p0*phi4/phi0;phi4:=1;p4_:=subs(dat,p4):'p4'=evalf(%,3); |
ADICIONAL. Respecto al aire ambiente, las variaciones de la humedad relativa con la presión para variaciones isotermas y para variaciones isoentrópicas son muy diferentes.
Isotérmicamente:
| > | eq8_7;get_pv_data(`gen`):'phi'=phi(w,T,p);Diff(phi,p)[w,T]=diff(rhs(%),p);get_pv_data(su2):Diff(phi,p)[w,T]=subs(dat,evalf(subs(p=p0,dat,diff(phi(w0_,T0,p),p)))):evalf(%,2);%*1e3; |
 |
![(Diff(phi, p))[w, T] = `/`(1, `*`(exp(`+`(A, `-`(`/`(`*`(B), `*`(`+`(T, C)))))), `*`(`+`(`/`(`*`(Mva), `*`(w)), 1))))](images/np52_29.gif) |
i.e. la phi aumenta casi un 0,7%/kPa.
isoentrópicamente, T/p^((ga-1)/ga)=cte.
| > | get_pv_data(`gen`):'phi'=phi(w,T,p);Diff(phi,p)[w,s]=diff(phi(w,T,p),p)+diff(phi(w,T,p),T)*dT_dp_isen;eqs:=T/p^((gamma-1)/gamma)=constant;eqs_logdif:=dT/T-((gamma-1)/gamma)*dp/p=0;dT_dp_isen:=(T/p)*(gamma-1)/gamma;get_pv_data(su2):Diff(phi,p)[w,s]=subs(T=T0,p=p0,w=w(phi0,T0,p0),dat,Adat,Wdat,diff(phi(w,T,p),p)+diff(phi(w,T,p),T)*dT_dp_isen):evalf(%,2);%*1e3; |
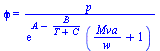 |
![(Diff(phi, p))[w, s] = `+`(`/`(1, `*`(exp(`+`(A, `-`(`/`(`*`(B), `*`(`+`(T, C)))))), `*`(`+`(`/`(`*`(Mva), `*`(w)), 1)))), `-`(`/`(`*`(B, `*`(T, `*`(`+`(gamma, `-`(1))))), `*`(exp(`+`(A, `-`(`/`(`*`(B...](images/np52_34.gif) |
i.e. la phi disminuye casi un 3%/kPa, ya que la disminución por efect térmico supera al aumento por efecto de la presión.
| > |