>	restart:#"m08_p51"

En una torre de enfriamiento evaporativo, se desea evacuar 1 MW de una corriente de agua que entra a 45 ºC y debe salir a 30 ºC, con aire atmosférico a 20 ºC y 30% de humedad relativa. Suponiendo que la presión es de 90 kPa, y que el aire a la salida va a estar a 25 ºC y 80%HR, se pide:
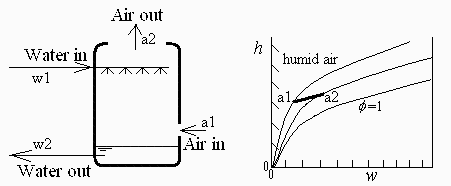
a) Esquema de la instalación y evolución del aire en el diagrama de Mollier h-w.
b) Balances másicos y energético de la torre de enfriamiento. Caudal de agua.
c) Estimar el gasto de agua por evaporación, suponiendo que todo el calor se invierte en evaporar la evaporación.
d) Humedad absoluta y entalpía unitaria del aire, a la entrada y a la salida.
e) Estimar el gasto de aire que hubiera sido necesario en un cambiador sin contacto aire/agua con las mismas temperaturas, y su valor en el caso de la torre.
f) Gasto medio de agua que sería necesario purgar, suponiendo que el agua de aporte tiene un concentración de sólidos disueltos de 0,5 g/kg y no se desea que sobrepase 10 g/kg.

Datos:

>	read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):

>	su1:="Aire":su2:="H2O":dat:=[Q=1e6*W_,Tw1=(45+273)*K_,Tw2=(30+273)*K_,Ta1=(20+273)*K_,phi1=0.3,Ta2=(25+273)*K_,phi2=0.8,p0=90e3*Pa_,yaporte=0.5e-3,ypurga=10e-3];

Esquema:

>

>

Eqs. const.:

>	Adat:=get_gas_data(su1):Adat:=subs(c[p]=c[pa],R=R[a],M=M[a],T[b]=nada,[Adat]):Wgdat:=get_gas_data(su2):Wgdat:=subs(c[p]=c[pv],R=R[v],M=M[v],[Wgdat]):Wldat:=get_liq_data(su2):Wdat:=op(Wgdat),Wldat:get_pv_data(su2):dat:=op(dat),Const,SI2,SI1:

a) Esquema de la instalación y evolución del aire en el diagrama de Mollier h-w.

Ver arriba.
b) Balances másicos y energético de la torre de enfriamiento. Caudal de agua

>	eqBMa:=ma1=ma2;eqBMw:=mw_evap=ma*(w2-w1);eqBEa:=Q=ma*(h2-h1);eqBEw:=Q=mw*cw*(Tw1-Tw2);mw_:=subs(dat,solve(subs(cw=c,dat,Wdat,%),mw));

Nota. Tomando la torre como sistema termodinámico, no hay transmisión de calor (todos los cambiadores se suponen adiabáticos en primera aproximación). El 'calor evacuado en la torre' se refiere al enfriamiento del gasto de agua de entrada (eqBEw).

c) Estimar el gasto de agua por evaporación, suponiendo que todo el calor se invierte en evaporar la evaporación.

>	eqBEwevap:=Q=mw_evap*h[lv0];mw_evap_:=subs(Wdat,dat,solve(%,mw_evap));

Nótese que el gasto evaporado es muy inferior al gasto de entrada.

d) Humedad absoluta y entalpía unitaria del aire, a la entrada y a la salida.

>	eq8_8;w1_:=evalf(subs(dat,w(phi1,Ta1,p0)));eq8_11;h1_:=subs(dat,Adat,Wdat,T=Ta1,dat,h(T,w1_));w2_:=evalf(subs(dat,w(phi2,Ta2,p0)));h2_:=subs(dat,Adat,Wdat,T=Ta2,dat,h(T,w2_));

Nota. Como de costumbre, se ha tomado el origen de entalpías en 0 ºC y 100 kPa tanto para el aire seco como para el agua líquida.

e) Estimar el gasto de aire que hubiera sido necesario en un cambiador sin contacto aire/agua con las mismas temperaturas, y su valor en el caso de la torre.

>	eqBEa_:=Q=ma*c[pa]*(Ta2-Ta1);ma_:=subs(dat,Adat,dat,solve(%,ma)):'ma'=evalf(%,2);eqBEa;ma_:=subs(dat,Q/(h2_-h1_));

Queda patente el interés de la torre: basta con soplar 26 kg/s en vez de 200 kg/s.

El agua realmente evaporada es:

>	mw_evap:='ma*(w2-w1)';mw_evap_:=ma_*(w2_-w1_);

Nótese que la primera aproximación (0,44 kg/s) no era muy mala.

f) Gasto medio de agua que sería necesario purgar, suponiendo que el agua de aporte tiene un concentración de sólidos disueltos de 0,5 g/kg y no se desea que sobrepase 10 g/kg.

Como no se evaporan los sólidos disueltos, el balance de éstos, en régimen estacionario, es:

>	eqBMs:=mw_aporte*yaporte-mw_purga*ypurga=0;mw_aporte=mw_evap;mw_purga_:=subs(dat,mw_evap_*yaporte/ypurga);

>