>	restart:#"m08_p43"

¿A qué temperatura sale en el equilibrio adiabático una mezcla de aire ambiente a 30 ºC y 60%HR, y agua fría, en función de la temperatura y el caudal de ésta?

Datos:

>	read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):

>	su1:="Aire":su2:="H2O":dat:=[T0=(30+273)*K_,phi0=0.6,mass_factor=1000,DTsa=5*K_];

Esquema:

>

>

Eqs. const.:

>	Adat:=get_gas_data(su1):Adat:=subs(c[p]=c[pa],R=R[a],M=M[a],T[b]=nada,[Adat]):Wgdat:=get_gas_data(su2):Wgdat:=subs(c[p]=c[pv],R=R[v],M=M[v],[Wgdat]):Wldat:=get_liq_data(su2):Wdat:=op(Wgdat),Wldat:get_pv_data(su2):dat:=op(dat),Const,SI2,SI1:

a) ¿A qué temperatura sale en el equilibrio adiabático una mezcla de aire ambiente a 30 ºC y 60%HR, y agua fría, en función de la temperatura y el caudal de ésta?

En las mezclas adiabáticas de agua y aire hay dos parámetros: la relación de gastos, mw_ma=mw/ma, y la temperatura de entradad del agua.

>

w0:=evalf(subs(dat,w(phi0,T0,p0))):'w0'=evalf(%,2);h0:=subs(dat,Adat,Wdat,T=T0,dat,h(T,w0)):'h0'=evalf(%,2);Tw:=subs(dat,T0);Tsa_:=(fsolve(subs(dat,Adat,Wdat,T=T0,dat,SI0,h(T,w(phi0,T,p0)))=subs(dat,Adat,Wdat,T=Tsa,SI0,h(T,w(1,T,p0))),Tsa=200..400))*K_:'Tsa0'=evalf(%,4);'Tsa0'=TKC(Tsa_);w0sa:=subs(dat,w(1,Tsa_,p0)):'wsa0'=evalf(%,2);hsa:=subs(dat,Adat,Wdat,T=Tsa_,dat,h(T,w0sa)):'hsa0'=evalf(%,2);mw_ma_sa:=w0sa-w0:'mw_ma_sa0'=evalf(%,2);

El aire ambiente a 30 ºC y 60%HR, en su saturación adiabática con agua a 30 ºC alcanzaría una temperatura de 23,5 ºC, tomando 2,6 g/kg de agua. Si tomara menos agua no llegaría a saturarse ni a enfriarse tanto, y si tomara más quedaría sobresaturado y tampoco se enfriaría tanto.

¿Cómo saldría si se añade muy poca agua (e.g. 1000 veces menos que la de saturación adiabática anterior)?

Pues que apenas importa su entalpía; simplemente se produce un ligero enfriamiento evaporativo.

¿Cómo saldría si se añade mucha más agua (e.g. 1000 veces más que la de saturación adiabática anterior) y muy fría (e.g. 5 ºC menos de la Tad)?

>

mw_ma:='mass_factor*mw_ma_sa';mw_ma:=subs(dat,mass_factor*mw_ma_sa):'mw_ma'=evalf(%,2);Tw:=Tsa0-DTsa;Tw_:=subs(dat,Tsa_-DTsa):'Tw'=evalf(%,3);'Tw'=TKC(Tw_);T2:=Tw_:eqBMw:='w0+mw_ma=w3+m4_ma';eqBMw:=w0+mw_ma=w3+m4_ma:eqBE:='h0+mw_ma*h2=h3+m4_ma*h4';eqBE:=subs(Wdat,h0+mw_ma*c*(T2-T[f])=h3+m4_ma*c*(T3-T[f])):w3:=w(1,T3,p0):h3:=subs(dat,Adat,Wdat,T=T3,dat,h(T,w3)):m4_ma:=mw_ma+w0-w3:T3_:=fsolve(subs(Adat,Wdat,dat,SI0,eqBE),T3=250..300)*K_:'T3'=evalf(%,3);'T3'=TKC(T3_);w3_:=subs(dat,w(1,T3_,p0)):'w3'=evalf(%,2);Dw:='w3-w0';Dw_:=w3_-w0:'Dw'=evalf(%,2);

i.e. si se le añade mucha (e.g. 1000 veces más de la de saturación) agua fría (e.g. a 18,5 ºC), la salida se acerca a esa temperatura, pero despacio porque la entalpía del líquido es pequeña. El enfriamiento del aire húmedo hace que condense algo de vapor (1,3 g/kg).

Si se añadiera mucha agua pero no muy fría (e.g. a 28,5 ºC):

>

Tw:=Tsa0+DTsa;Tw_:=subs(dat,Tsa_+DTsa):'Tw'=evalf(%,3);'Tw'=TKC(Tw_);T2:=Tw_:w3:='w3':h3:='h3':m4_ma:='m4_ma':eqBMw:='w0+mw_ma=w3+m4_ma';eqBMw:=w0+mw_ma=w3+m4_ma:eqBE:='h0+mw_ma*h2=h3+m4_ma*h4';eqBE:=subs(Wdat,h0+mw_ma*c*(T2-T[f])=h3+m4_ma*c*(T3-T[f])):w3:=w(1,T3,p0):h3:=subs(dat,Adat,Wdat,T=T3,dat,h(T,w3)):m4_ma:=mw_ma+w0-w3:T3__:=fsolve(subs(Adat,Wdat,dat,SI0,eqBE),T3=250..350)*K_:'T3'=evalf(%,4);'T3'=TKC(T3__);w3__:=subs(dat,w(1,T3__,p0)):'w3'=evalf(%,2);Dw:='w3-w0';Dw_:=w3__-w0:'Dw'=evalf(%,2);

i.e. la salida se acerca a esa nueva temperatura de entrada del agua, pero despacio porque la entalpía del líquido es pequeña. Ahora el aire disuelve mucho más vapor (7 g/kg).

>	plot(subs(dat,SI0,[[w(1,T,p0),T-273,T=273..313],[[w0,T0-273],[w0sa,Tsa_-273]],[[w0sa,Tsa_-273],[w3_,T3_-272.5]],[[w0sa,Tsa_-273],[w3__,T3__-272.5]],[[0,Tsa_+DTsa-273],[1,Tsa_+DTsa-273]],[[0,Tsa_-DTsa-273],[1,Tsa_-DTsa-273]]]),w=0..0.03,T=0..40,color=black);

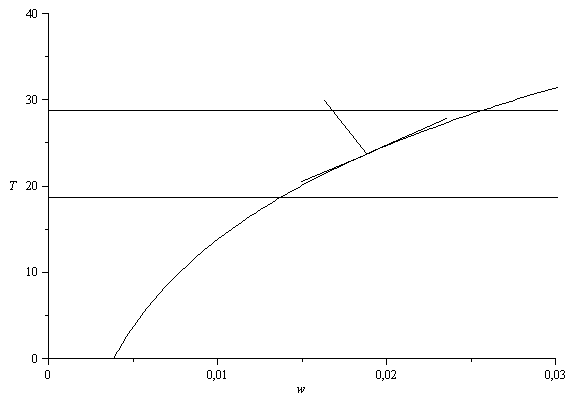i.e.:

Para mw<<ma<<1 la Tsalida=Tad independientemente de la Tentrada_agua.

Para mw>>ma, la Tsalida se aproxima por debajo a la Tentrada_agua si es alta y por encima si es baja (porque en lugar de enfriamiento evaporativo es calentamiento condensativo).

Nótese que aquí sólo se ha estudiado la entrada y la salida y no los detalles del proceso, por lo que sólo se puede esbozar el camino en el diagrama psicrométrico (una curva suave entre la entrada y la salida, acercándose algo al punto de saturación adiabática normal).

>