>	restart;#"m08_p40"

Se trata de analizar la mezcla binaria de N2 y H2O como modelo para el estudio del aire húmedo  Se pide:
a) Construir el diagrama T-x a presión ambiente de las mezclas bifásicas´(líquido-vapor) de N2 y H2O, suponiendolas ideales y sin más cambios de fase.
b) Determinar la composición de las fases saturadas a 288 K.
c) Indicar la utilidad del modelo.

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):

>	su1:="N2":su2:="H2O":dat:=[T_=288*K_];

Esquema:

>

Eqs. const.:

>	g1dat:=get_gas_data(su1):l1dat:=get_liq_data(su1):g2dat:=get_gas_data(su2):l2dat:=get_liq_data(su2):dat1:=op(dat),g1dat,l1dat,Const,SI2,SI1:dat2:=op(dat),g2dat,l2dat,Const,SI2,SI1:pv1:=proc(T) global su1;get_pv_data(su1);RETURN(pv(T)):end:pv2:=proc(T) global su1;get_pv_data(su2);RETURN(pv(T)):end:

Equilibrio binario líquido-vapor:

>	eqNV:=xv1+xv2=1;eqNL:=xl1+xl2=1;eqC1:=xv1*xv0+xl1*xl0=x01;eqC2:=xv2*xv0+xl2*xl0=x02;eqE1:=xv1/xl1=pv1/p;eqE2:=xv2/xl2=pv2/p;sol1:=solve({eqNV,eqNL,eqE1,eqE2},{xv1,xv2,xl1,xl2});sol2:=solve({eqC1,eqC2},{xv0,xl0});

a) Construir el diagrama T-x a presión ambiente de las mezclas bifásicas´(líquido-vapor) de N2 y H2O, suponiendolas ideales y sin más cambios de fase.
El intervalo de temperatura en el que podría haber mezcla bifásica de nitrógeno y agua, si no se conocieran las concentraciones, estaría limitado por las de ebullición puras.

>	T1_:=evalf(subs(dat1,solve(p0=pv1(T),T))):'T1'=evalf(%,3);T2_:=evalf(subs(dat2,solve(p0=pv2(T),T))):'T2'=evalf(%,3);

Diagrama T-x:

>

n:=19:for i from 0 to n do T||i:=T1_+(T2_-T1_)*(i/n);xv1||i:=subs(sol1,p=p0,pv1=pv1(T||i),pv2=pv2(T||i),dat1,SI0,xv1);xl1||i:=subs(sol1,p=p0,pv1=pv1(T||i),pv2=pv2(T||i),dat1,SI0,xl1);od:plot({[seq([xv1||i,T||i/K_],i=0..n)],[seq([xl1||i,T||i/K_],i=0..n)],[[0,T2_/K_],[.2,T2_/K_]],[[1,T1_/K_],[.8,T1_/K_]],subs(dat,[[0,T_/K_],[1,T_/K_]])},x[N2]=0..1,'T_K'=0..400,color=black,axes=boxed);

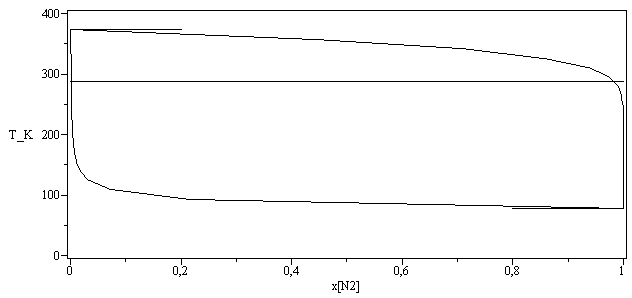b) Determinar la composición de las fases saturadas a 288 K.

>	subs(dat1,evalf(subs(T=T_,dat,{pv1=pv1(T),pv2=pv2(T)}))):evalf(%,3);subs(dat1,evalf(subs(p=p0,pv1=pv1(T),pv2=pv2(T),T=T_,dat,sol1))):evalf(%,3);

c) Indicar la utilidad del modelo.

Sólo es válido para la fase gaseosa, cuyo límite es muy aproximadamente la temperatura de rocío; i.e. la la xv de saturación a 15 ºC sí es xv=0,17.

Ya la composición de la fase condensada no es buena: la de saturación a 15 ºC sale 1,4*10^-3 y sin embargo es de 1*10^-5.

El haber considerado el aire seco como N2 puro no está mal, y eso que el oxígeno se disuelve en agua el doble que el nitrógeno.

Por debajo de 0º C el agua congela y ya no sirve el modelo.

>