>	restart:#"m08_p38"

En un frasco de vidrio de 10 litros se introduce aire ambiente (con una bomba de bicicleta, a través del tapón) hasta que en un manómetro en U conectado al tapón, una vez atemperado todo, se alcanza 1 m de columna de agua de desnivel, todo ello en un ambiente a 22 ºC, 93 kPa y 70% de humedad. Después, se pone rápidamente en comunicación el interior con el exterior (a través de una llave de paso). Se pide:
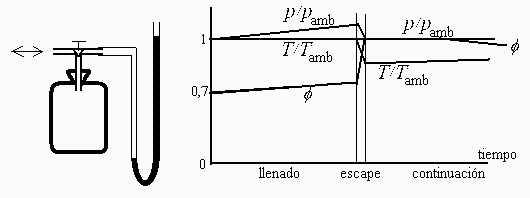
a) Esquema de la instalación y de la evolución esperada de la presión, temperatura y humedad interiores durante el llenado, el escape y la continuación.
b) Determinar la cantidad de vapor y la humedad relativa justo antes de la despresurización (estado 1).  
Determinar la humedad relativa inmediatamente después de la despresurización (estado 2).

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):

>	su1:="Aire":su2:="H2O":dat:=[V=0.01*m_^3,Dp01=(1/10)*1e5*Pa_,T0=(22+273)*K_,p0=93e3*Pa_,phi0=0.7];

Esquema:

>

>

Eqs. const.:

>	Adat:=get_gas_data(su1):Adat:=subs(c[p]=c[pa],R=R[a],M=M[a],T[b]=nada,[Adat]):Wgdat:=get_gas_data(su2):Wgdat:=subs(c[p]=c[pv],R=R[v],M=M[v],[Wgdat]):Wldat:=get_liq_data(su2):Wdat:=op(Wgdat),Wldat:get_pv_data(su2):dat:=op(dat),Const,SI2,SI1:

a) Esquema de la instalación y de la evolución esperada de la presión, temperatura y humedad interiores durante el llenado, el escape y la continuación.

De 0 a 1 va aumentando la presión. Por sencillez, supondremos que lo hace lentamente, y por tanto la temperatura apenas variará, mientras que la humedad relativa irá aumentando por el efecto de la presión (la absoluta permanece constante).

De 1 a 2, se enfría isoentrópicamente y la humedad relativa seguirá aumentando porque el enfriamiento impera sobre la disminución de presión.

Al cabo del tiempo se irá atemperando a presión ambiente y la humedad tenderá a volver a la del ambiente.

b) Determinar la cantidad de vapor y la humedad relativa justo antes de la despresurización (estado 1).  

>

p1:=p0+Dp01;p1_:=subs(dat,p1):'p1'=evalf(%,3);T1:=T0;w1:=w0;w1_:=evalf(subs(dat,w(phi0,T0,p0))):'w1'=evalf(%,3);phi1:='phi0*p1/p0';phi1_:=subs(dat,phi1):'phi1'=evalf(%,2);na1:='p1*V/(R[u]*T1)';na1_:=subs(dat,na1):'na1'=evalf(%,3);xv1:='phi1_*pv1/p1';pv1:=subs(dat,evalf(subs(dat,pv(T1)))):'pv1'=evalf(%,3);xv1_:=subs(dat,xv1):'xv1'=evalf(%,3);nv1:='xv1*na1';nv1_:=subs(dat,nv1):'nv1'=evalf(%,3);mv1_:=subs(Wdat,nv1_*M[v]):'mv1'=evalf(%,3);

c) Determinar la cantidad de vapor inmediatamente después de la despresurización (estado 2), su temperatura y la humedad relativa, en cualquiera de los dos supuestos anteriores.

Al ser la despresurización rápida y sin fricción, el gas se enfriar isoentrópicamente.

Si suponemos que no llega a condensar el vapor y aproximamos las propiedades del aire húmedo por las del aire seco:

>

T2:=T1*(p2/p1)^((gamma-1)/gamma);p2:=p0;T2_:=subs(Adat,dat,T2):'T2'=evalf(%,3);xv2:='xv1';na2:='p2*V/(R[u]*T2_)';na2_:=subs(dat,na2):'na2'=evalf(%,3);nv2:='xv2*na2';nv2_:=subs(dat,nv2):'nv2'=evalf(%,3);mv2_:=subs(Wdat,nv2_*M[v]):'mv2'=evalf(%,3);phi2:='xv2*p2/pv2';pv2:=subs(dat,evalf(subs(dat,pv(T2_)))):'pv2'=evalf(%,3);phi2_:=subs(dat,phi2):'phi2'=evalf(%,3);

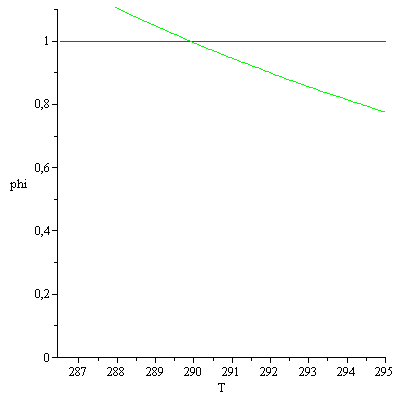
luego s que condesa una parte, quedando la fase gaseosa saturada (phi2=1) y a temperatura algo superior, pero inferior a la de saturación (i.e. entre 286,5 K y 288 K).

>	phi_:=subs(Adat,dat,SI0,xv2*p1*(T/T1)^(gamma/(gamma-1))/pv(T)):'phi'=evalf(%,3);Taux:=fsolve(phi_=1,T=200..400)*K_:'Taux'=evalf(%,3);plot([1,phi_],T=subs(SI0,T2_)..subs(dat,SI0,T1),phi=0..1.1);

Si se supone que ambas fases siguen en equilibrio, la temperatura (y la masa condensada) podría estimarse como la de saturación con la misma entalpía del estado metastable 2.

>

h2_:=subs(Adat,Wdat,T=T2_,dat,h(T,w1_)):'h2'=evalf(%,3);T2eq_:=fsolve(subs(Adat,Wdat,dat,SI0,h2_=h(T,w(1,T,p0))),T=200..400)*K_:'T2eq'=evalf(%,4);w2eq_:=evalf(subs(dat,w(1,T2eq_,p0))):'w2eq'=evalf(%,3);mv2eq:='w2eq_*na2_*M[a]';mv2eq_:=subs(Adat,dat,mv2eq):'mv2eq'=evalf(%,2);mw2eq:='mv2-mv2eq';mw2eq_:=mv2_-mv2eq_:'mw2eq'=evalf(%,2);wf_cond:='mw2eq/mv2';wf_cond_:=evalf((mw2eq_/mv2_)*100*mass_percent_of_liquid,2);

>