>	restart:#"m08_p30"

A una corriente de aire en condiciones ambiente de 20 ºC, 90 kPa y 50% de humedad relativa (estado A), se le añade un flujo de vapor de agua saturado a esa misma presión (estado B), saliendo la mezcla también a esa presión (estado C).  Sea m la relación de gastos másicos de las corrientes de vapor y aire Se pide:
a) Determinar las densidades en los estados A y B.
b) Supóngase que el estado C consiste sólo en aire húmedo saturado y determínese la humedad absoluta y la temperatura correspondiente en función de m (con aplicación numérica para m=10-3, 10-2  y 10-1).
c) Establecer el balance energético y calcular el intercambio térmico que sería necesario para que se cumpliera la hipótesis anterior (calor a aportar por unidad de gasto másico de aire seco).
d) Sabiendo que el proceso real es rápido, indicar cómo se determinaría realmente el estado C.
Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):with(plots):

>	su1:="Aire":su2:="H2O":dat:=[T0=(20+273)*K_,p0=90e3*Pa_,phi0=0.5];

Warning, the name changecoords has been redefined

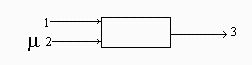
Esquema:

>

>

Eqs. const.:

>	eqET:=eq1_12;Adat:=get_gas_data(su1):Adat:=subs(c[p]=c[pa],R=R[a],M=M[a],T[b]=nada,[Adat]):Wgdat:=get_gas_data(su2):Wgdat:=subs(c[p]=c[pv],R=R[v],M=M[v],[Wgdat]):Wldat:=get_liq_data(su2):Wdat:=op(Wgdat),Wldat:get_pv_data(su2):dat:=op(dat),Const,SI2,SI1:

a) Determinar las densidades en los estados A y B

>

eqBMw:=w1+mu=w3;eqBE:=h1+mu*h2+q=h3;rho1:=subs(dat,subs(p=p0,T=T0,R=R[a],dat,Adat,rhs(eqET))):'rho1'=evalf(%,2);T2:=Tvp0;T2_:=subs(dat,solve(subs(dat,p0=pv(T)),T)):'T2'=evalf(%,3);T2_C:=(T2_/K_-273)*`ºC`:'T2'=evalf(%,2);rho2:=subs(dat,subs(p=p0,T=T2_,R=R[v],dat,Wdat,rhs(eqET))):'rho2'=evalf(%,2);w1_:=evalf(subs(dat,w(phi0,T0,p0))):'w1'=evalf(%,2);Tr1_:=solve(subs(dat,pv(T)=phi0*pv(T0)),T):'Tr1'=evalf(%,3);Tr1_C:=(Tr1_/K_-273)*`ºC`:'Tr1_C'=evalf(%,2);h1_:=subs(dat,Adat,Wdat,T=T0,dat,h(T,w1_)):'h1'=evalf(%/(1e3*J_/kJ_),2);h2_:=subs(c[p]=c[pv],dat,Wdat,T=T2_,dat,hv(T)):'h2'=evalf(%/(1e6*J_/MJ_),2);

b) Supóngase que el estado C consiste sólo en aire húmedo saturado y determínese la humedad absoluta y la temperatura correspondiente en función de m (con aplicación numérica para m=10-3, 10-2  y 10-1 .

>

'phi3'=1;w3:=subs(dat,w(1,T,p0)):'w3'=evalf(%,2);eqBMw_:=subs(w1=w1_,dat,eqBMw):'eqBMw'=evalf(%,2);T3_:=solve(eqBMw_,T):w3_:=subs(T=T3_,w3):eqBE_:=subs(h1=h1_,h2=h2_,h3=h(T,w3),mu=mu_,Adat,Wdat,dat,eqBE):'eqBE'=evalf(%,2);q_:=subs(T=T3_,mu_=mu,dat,solve(eqBE_,q)):for mu in [1e-3,1e-2,1e-1] do T3__:=evalf(T3_);w3__:=evalf(w3_);q__:=evalf(q_):print('mu'=mu,'T3'=evalf(T3__,3),'w3'=evalf(w3__,2),'q'=evalf(q__,2));od:

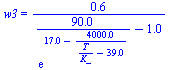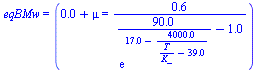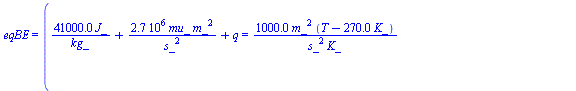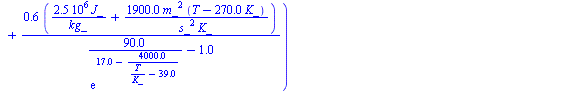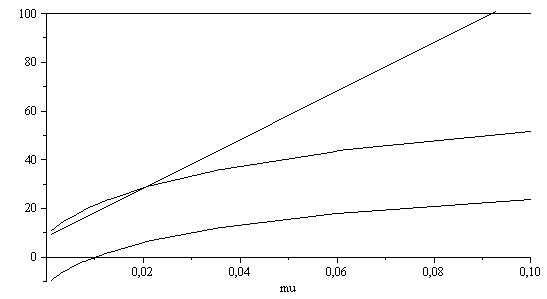
c) Establecer el balance energético y calcular el intercambio térmico que sería necesario para que se cumpliera la hipótesis anterior (calor a aportar por unidad de gasto másico de aire seco).

>

mu:='mu':n:=10:arr:=array(1..n,1..4):for i from 1 to n do mu:=10^(-3+2*((i-1)/(n-1)));arr[i,1]:=mu;arr[i,2]:=evalf(T3_/K_-273);arr[i,3]:=evalf(subs(SI0,q_/1000));arr[i,4]:=evalf(w3_*1000);od:plot([pla(arr,2,1),pla(arr,3,1),pla(arr,4,1),100],'mu'=0..0.1,-10..100,color=black);mu:='mu':mu_q_0:=solve(q_=0,mu):'mu_q_0'=evalf(%,1);

d) Sabiendo que el proceso real es rápido, indicar cómo se determinaría realmente el estado C

Entonces q=0 y saldrá sin saturar si cuando antes daba q<0 o sobresaturado si q>0.

Si no se satura:

>	h3_:=h1_+mu*h2_;w3_:=w1_+mu:'w3_'=evalf(%,2);T3_:=subs(dat,solve(subs(mu=mu_,Adat,Wdat,dat,mu_=mu,h3_=h(T,w3_)),T));phi3_:=subs(mu=mu_,Wdat,dat,mu_=mu,phi(w3_,T3_,p0)):for mu in [1e-3,1e-2,1e-1] do print('mu'=mu,'T3'=evalf(T3_,3),'w3'=evalf(w3_,2),'phi3'=evalf(phi3_,3));od:

>

n:=10:arr:=array(1..n,1..5):for i from 1 to n do mu:=0+(mu_q_0)*((i-1)/(n-1));arr[i,1]:=mu;arr[i,2]:=T3_/K_-273;arr[i,3]:=phi3_*100;arr[i,4]:=(w1_+mu)*1000;arr[i,5]:=0:od:mu:='mu':mu_phi_1:=solve(phi3_=1,mu):'mu_phi_1'=evalf(%,1);pl1:=plot([pla(arr,2,1),pla(arr,3,1),pla(arr,4,1)],'mu'=0..mu_q_0,0..100,color=black):

A partir de mu=mu_phi_1 se satura y entonces:

>

arr_:=array(1..n,1..5):arr_:=evalm(arr):w3:='w3':w3_:=subs(dat,w(1,T,p0)):'w3'=evalf(%,2);h3_:=subs(dat,Adat,Wdat,h(T,w3_)):'h3'=evalf(%,2);eqBMw:=w1+mu=w3+beta;beta_:=w1_+mu-w3_:eqBE:=h1+lambda*h2=h3+beta*h4;h4_:=subs(dat,Wdat,c*(T-T[tr]));for mu in [1e-3,1e-2,1e-1] do T3_:=fsolve(subs(mu=mu_,dat,Adat,Wdat,SI0,h1_+mu*h2_=h3_+beta_*h4_),T=200..500)*K_:'T3'=evalf(%,3);w3__:=evalf(subs(dat,T=T3_,w3_)):'w3'=evalf(%,2);beta__:=w1_+mu-w3__:'beta'=evalf(%,2);phi3_:=subs(dat,phi(w3__,T3_,p0)):'phi3'=evalf(%,3);beta__:=evalf(subs(T=T3_,beta_));print('mu'=mu,'T3'=evalf(T3_,3),'w3'=evalf(w3__,2),'beta'=evalf(beta__,2));od:mu:='mu':mu_beta_0:=solve(subs(T=T3_,beta_)=0,mu):'mu_beta_0'=evalf(%,1);

>

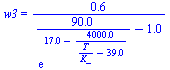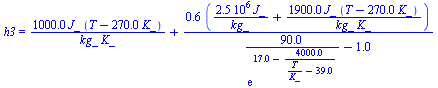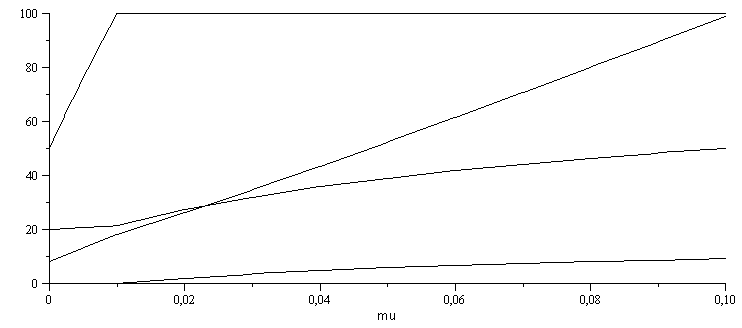
for i from 1 to n do mu_:=mu_q_0+(.1-mu_q_0)*((i-1)/(n-1));T3_:=fsolve(subs(mu=mu_,dat,Adat,Wdat,SI0,h1_+mu_*h2_=h3_+beta_*h4_),T=273..373)*K_;w3__:=evalf(subs(mu=mu_,dat,T=T3_,w3_));beta__:=w1_+mu_-w3__;arr[i,1]:=mu_;arr[i,2]:=T3_/K_-273;arr[i,3]:=w3__*1000;arr[i,4]:=beta__*1000;arr[i,5]:=100:od:pl2:=plot([pla(arr,2,1),pla(arr,3,1),pla(arr,4,1),pla(arr,5,1)],'mu_'=mu_q_0..0.1,0..100,color=black):display([pl1,pl2]);

>