>	restart:#"m07_p48"

Un depósito de 0,25 m3 contiene inicialmente O2 a 5 ºC y 520 kPa, el cual se pone en comunicación a través de una pequeña línea con un depósito de 2 m3 de N2 inicialmente a 25 ºC y a 250 kPa. Se pide:

a) Determinar la composición final tras el atemperamiento en un ambiente a 25 ºC.

b) Intercambio energético con el exterior, y generación de entropía en el proceso.

c) Determinar la composición inmediatamente después del equilibrio mecánico (antes del atemperamiento).

d) Intercambio energético con el exterior y generación de entropía en este último caso.

e) Intercambio energético con el exterior y generación de entropía en el atemperamiento posterior.

Datos:

>	read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):Digits:=5:with(plots):

>	su1:="O2":su2:="N2":dat:=[V1=0.25*m_^3,T1=(5+273.15)*K_,p1=520e3*Pa_,V2=2*m_^3,T2=(25+273.15)*K_,p2=250e3*Pa_,T0=(25+273.15)*K_];

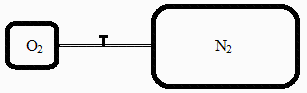
Sea O=O2, N=N2, 1=Dep1, 2=Dep2, i=ini, f=fin.

Usaremos variables molares para aprovechar que, como ambos gases son diatómicos, tendrán casi las mismas propiedades térmicas.

>	Odat:=get_gas_data(su1):Ndat:=get_gas_data(su2):c[p,O2]:=subs(Odat,c[p]*M);c[p,N2]:=subs(Ndat,c[p]*M);dat:=cp=(7/2)*R,cv=(5/2)*R,R=8.314*J_/(mol_*K_),gamma=1.4,op(dat),Const,SI2,SI1:c[p]=subs(dat,cp);c[v]=subs(dat,cv);

	(1)

a) Determinar la composición final tras el atemperamiento en un ambiente a 25 ºC.

Cantidades iniciales y finales. La presión final se halla con los moles totales en el volumen total.

>	eqE:=p*V=n*R*T;nO1i:=p1*V1/(R*T1);nO1i_:=subs(dat,%);nN1i:=0;nO2i:=0;nN2i:=p2*V2/(R*T2);nN2i_:=subs(dat,%);Cond_Fin:=nN1f=0,T1f=T2f,p1f=p2f,pf*Vtot=ntot*R*T0;eqpf:=pf='(nO1i+nN2i)*R*T0/(V1+V2)';eqpf_:=subs(dat,%);nO1f:=pf*V1/(R*T0);nO1f_:=subs(eqpf_,dat,%);nO2f_:=nO1i_-nO1f_;nN2f_:=nN2i_;

	(2)

i.e. al inicio hay 56 mol de O2 en V1 y 202 mol de N2 en V2. Al final ambos depósitos quedan a 284 kPa, el V1 con 29 mol de O2, y el V2 con 28 mol de O2 que han entrado, más los 202 mol de N2 iniciales.

b) Intercambio energético con el exterior, y generación  de entropía en el proceso.

Considerando el conjunto, no hay trabajo por ser rígido, y el calor que entra será:

>	eqBE:=DE=Q+W;eqBE:=Q=Uf-Ui;eqBE:=Q='nO1i*cv*(T0-T1)+nN2i*cv*(T0-T2)';Q_:=subs(dat,nO1i*cv*(T0-T1)+nN2i*cv*(T0-T2));Q0_:=-Q_;

	(3)

i.e. entran 23,4 kJ de calor desde el ambiente. El detalle para cada depósito sería más complicado (ver abajo).

Para la entropía conviene operar con presiones parciales para no tener que añadir el término de entropía de mezclado.

Hay que considerar 3 subsistemas interiores (nO1f, nO2f, y nN2) y el ambiente.

>

Sgen:=DSuniv;Sgen:=DSnO1f+DSOn2f+DSnN+DS0;DSnO1f:='nO1f*(cp*ln(T0/T1)-R*ln(pf/p1))';DSnO2f:='nO2f*(cp*ln(T0/T1)-R*ln(xO2f*pf/p1))';DSnN:='nN2i*(cp*ln(T0/T2)-R*ln(xN2f*pf/p2))';DS0:=Q0/T0;DS0_:=subs(dat,Q0_/T0);xO2f:=nO2f/(nO2f+nN2f);xO2f_:=subs(nO2f=nO2f_,nN2f=nN2f_,dat,%);xN2f_:=1-%;DSnO1f_:=subs(dat,evalf(subs(eqpf_,dat,DSnO1f)));DSnO2f_:=subs(dat,evalf(subs(eqpf_,nO2f=nO2f_,nN2f=nN2f_,dat,DSnO2f)));DSnN_:=subs(dat,evalf(subs(eqpf_,nN2f=nN2f_,xN2f=xN2f_,dat,DSnN)));Sgen_:=DSnO1f_+DSnO2f_+DSnN_+DS0_;

	(4)

i.e. la entropía del ambiente disminuye, pero la del interior aumenta más, y para el conjunto DSuniv=800 J/K.

c) Determinar la composición inmediatamente después del equilibrio mecánico (antes del atemperamiento).

Antes de la transmisión de calor, el V1 habrá sufrido una descarga isentrópica (rápida y sin fricción), mientras que el V2 sufrirá un llenado rápido y con fricción. La nueva pf será distinta.

Para el sistema abierto V1:

>	nO1f:='nO1f':eqBE1:=p*v^gamma=cte;eqBE1:=p*(1/n)^gamma=cte;eqBE1:=nO1f='nO1i*(pf/p1)^(1/gamma)';eqBE1_:=T1f=T1*(pf/p1)^((gamma-1)/gamma);

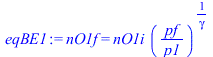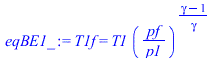	(5)

Para el sistema conjunto V1+V2 (cerrado, rígido y adiabático), considerando los 3 subsistemas interiores (nO1f, nO2f, y nN2)

>	nN2i:='nN2i':eqBE2:=DUO1f+DUO2f+DUN2=0;DUO1f:=nO1f*cv*(T1f-T1);DUO2f:=nO2f*cv*(T2f-T1);DUN2:=nN2i*cv*(T2f-T2);

	(6)

Hay 2 incógnitas, pf,  y Tf2, y las 2 ecuaciones son el BE2 y la ecuación de estado en V2. Se reduce a una ecuación substituyendo T2f(pf) en el BE2, y se resuelve numéricamente (como V2>>V1, la pf será próima y algo por encima de la p2ini).

>

eqET2:=pf*V2=(nO2f+nN2i)*R*T2f;eqET2_:=subs(nO2f=nO1i_-nO1f,nN2i=nN2i_,eqBE1,dat,SI0,eqET2);eqBE2_:=subs(nO2f=nO1i_-nO1f,nN2i=nN2i_,eqBE1,eqBE1_,dat,SI0,eqBE2);sol_:=fsolve({eqET2_,eqBE2_},{pf,T2f});pf_:=subs(sol_,pf)*Pa_;T2f_:=subs(sol_,T2f)*K_;T1f_:=subs(pf=pf_,dat,rhs(eqBE1_));nO1f_:=subs(pf=pf_,dat,rhs(eqBE1));

	(7)

i.e. antes de atemperarse la presión de equilibrio es de 280 kPa (en vez de 284 kPa), las temperaturas son T1f=233 K y T2f=304 K (que luego se atemperarán a T0=298 K), y quedan 36 mol de O2 en el V1 (pasando los otros 20 mol de O2 del V1 al V2 en este procso, y luego pasarán otros 8 mol de O2 durante el atemperaminto).

ADICIONAL

d) Intercambio energético con el exterior y generación de entropía en este último caso.

No hay trabajo con el exterior por ser rígido, ni calor por ser rápido. Para la entropía basta ahora considerar 2 subsistemas, el nO2f y el nN2, pues el nO1f ha sufrido un proceso isentrópico, y el ambiente no ha participado.

>

W=0;Q=0;xO2f:='xO2f':Sgen:=DSuniv;Sgen:='DSnO1f+DSOn2f+DSnN+DS0';DSnO1f:=0;DSnO2f:=nO2f*(cp*ln(T0/T1)-R*ln(xO2f*pf/p1));DSnN:='nN2i*(cp*ln(T0/T2)-R*ln(xN2f*pf/p2))';DS0:=0;xO2f:=nO2f/(nO2f+nN2f);xO2f_:=subs(nO2f=nO1i_-nO1f_,nN2f=nN2i_,dat,%);xN2f_:=1-%;DSnO2f_:=subs(dat,evalf(subs(pf=pf_,nO2f=nO2f_,nN2f=nN2f_,dat,DSnO2f)));DSnN_:=subs(dat,evalf(subs(pf=pf_,nN2i=nN2i_,xN2f=xN2f_,dat,DSnN)));Sgen_:=DSnO2f_+DSnN_;

	(8)

i.e. hasta el equilibrio mecánico ya se han generado 652 J/K de los 803 J/K totales hasta el atemperamiento.

e) Intercambio energético con el exterior y generación de entropía en el atemperamiento posterior.

Tras el equilibrio mecánico, el depósito pequeño queda con O2 frío (a 233 K), y el grande queda con una mezcla caliente (a 304 K), por lo que el primero recibirá calor de exterior (de las paredes del tanque, y estas del ambiente exterior), mientras que el grande cederá calor al exterior (a las paredes del tanque y estas al exterior). El cálculo de estos flujos de calor se complica porque cada depósito es un sistema abierto en régimen no estacionario.

Podemos hacer una simulación numérica de la transmisión de calor poniendo Qdot=K*A*DT, con unas Ks típicas de 10 W/(m2·K) y unas áreas correspondientes a depósitos esféricos (aunque la forma no influye mucho).

>

eqHT1:=dQ1=K1*A1*(T0-T1);eqHT1:=dQ2=K2*A2*(T0-T2);eqBE1:=d(nO1*c[v]*T1)=dQ1+c[p]*T1*dnO1;eqBE2:=d((nt-no1)*c[v]*T2)=dQ2-c[p]*T1*dnO1;eqp:=nO1*R*T1/V1=(nt-nO1)*R*T2/V2;n_:=solve(%,nO1);eqAVcube:=A=6*L^2,V=L^3,A=6*V^(2/3);eqAVsphere:=A=Pi*D^2,V=Pi*D^3/6,A=V^(2/3)*Pi*(6/Pi)^(2/3),A=4.84*V^(2/3),f=4.84,A=f*V^(2/3);

	(9)

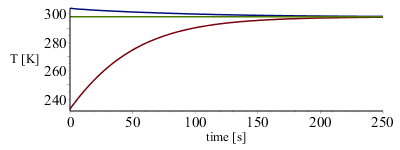
El resultado numérico para la evolución temporal de las temperaturas de cada depósito es (para K1=K2=10 basta un tiempo total de simulación de ttot=250 s; para menor K mayor ttot):

>

dat_:=K1=10,K2=10,ttot=250,V1=0.25,V2=2,A1=4.84*0.25^(2/3),A2=4.84*2^(2/3),c[v]=(5/2)*8.3,c[p]=(7/2)*8.3,R=8.3,T0=298,nt=258;K1=subs(dat_,K1*W_/(m_^2*K_)),K2=subs(dat_,K2*W_/(m_^2*K_));eqBE1_:='diff(n(t)*c[v]*T1(t),t)'=K1*A1*(T0-T1(t))+c[p]*T1(t)*diff(n(t),t);eqBE2_:='diff((nt-n(t))*c[v]*T2(t),t)'=K2*A2*(T0-T2(t))-c[p]*T1(t)*diff(n(t),t);eqn:=n(t)=nt*V1*T2(t)/(V1*T2(t)+V2*T1(t));eqs_:=simplify(expand(subs(eqn,dat_,[eqBE1_,eqBE2_]))):sol_:=dsolve({op(eqs_),T1(0)=233,T2(0)=304},numeric);odeplot(sol_,[[t,T1(t)],[t,T2(t)],[t,298]],t=0..subs(dat_,ttot),labels=["time [s]","T [K]"]);

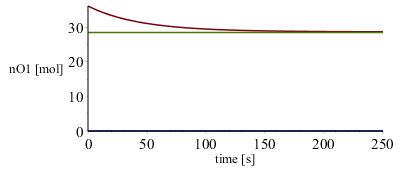
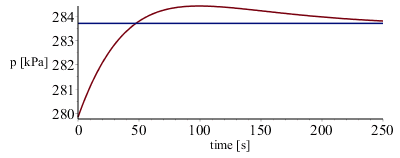
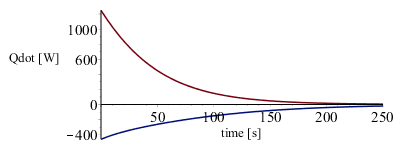
La presión, la contidad de O2 que queda en V1, y los flujos de calor, evolucionan así:

>

odeplot(sol_,[[t,subs(dat_,rhs(eqn))],[t,0],[t,28.5]],t=0..subs(dat_,ttot),labels=["time [s]","nO1 [mol]"]);odeplot(sol_,[[t,subs(dat_,rhs(eqn))*8.3*T1(t)/250],[t,283.7]],t=0..subs(dat_,ttot),labels=["time [s]","p [kPa]"]);odeplot(sol_,[[t,subs(dat_,K1*A1*(T0-T1(t)))],[t,subs(dat_,K2*A2*(T0-T2(t)))]],t=0..subs(dat_,ttot),labels=["time [s]","Qdot [W]"]);sol_(0);Dt:=2:dQ1:=seq(subs(dat_,K1*A1*(T0-op(2,sol_(i*Dt)[2]))),i=0..subs(dat_,ttot/Dt)):Q1:=convert([%],`+`)*Dt*J_;dQ2:=seq(subs(dat_,K2*A2*(T0-op(2,sol_(i*Dt)[3]))),i=0..subs(dat_,ttot/Dt)):Q2:=evalf(convert([%],`+`))*Dt*J_;Q:=Q1+Q2;

	(10)

que se han integrado para determinar el calor total que entra en el V1, 61 kJ, y el que sale del V2, 38 kJ, y comparar el valor neto (23 kJ) con el obtenido al principio (23,4 kJ), en el segundo apartado.

La generación de entropía en cada depósito se podría resolver de un modo similar, pero la del conjunto será simplemente la del proceso global (Sgen=800 J/K) menos la del proceso inicial hasta el equilibrio mecánico (Sgen=652 J/K), i.e. 800-652=148 J/K; se aprecia que la mayor parte tiene lugar al principio.

>