>	restart:#"m07_p43"

En un recipiente de 50 L hay 20 kg de mezcla propano/butano equimolar, a 500 kPa, en un ambiente a 94 kPa y 20 ºC. Se pide:

a) Diagramas esquemáticos T-x y p-x de todas las mezclas posibles a esa presión y esa temperatura, respectivamente, indicando los valores de los extremos (sustancias puras).  

b) Composición en el interior (fracciones molares de cada fase).

c) Masa de vapor.

Datos:

>	read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):Digits:=5:

>	su1:="C3H8":su2:="C4H10":dat:=[V=0.05*m_^3,mtot=20*kg_,x01=0.5,x02=0.5,p1=500e3*Pa_,p0=94e3*Pa_,T0=(20+273.15)*K_];

>	g1dat:=get_gas_data(su1):l1dat:=get_liq_data(su1):g2dat:=get_gas_data(su2):l2dat:=get_liq_data(su2):dat1:=op(dat),g1dat,l1dat,Const,SI2,SI1:dat2:=op(dat),g2dat,l2dat,Const,SI2,SI1:pv1:=proc(T) global su1;get_pv_data(su1);RETURN(pv(T)):end:pv2:=proc(T) global su1;get_pv_data(su2);RETURN(pv(T)):end:

>	eqNV:=xv1+xv2=1;eqNL:=xl1+xl2=1;eqC1:=xv1*xv0+xl1*xl0=x01;eqC2:=xv2*xv0+xl2*xl0=x02;eqE1:=xv1/xl1=pv1/p;eqE2:=xv2/xl2=pv2/p;sol1:=solve({eqNV,eqNL,eqE1,eqE2},{xv1,xv2,xl1,xl2});sol2:=solve({eqC1,eqC2},{xv0,xl0});

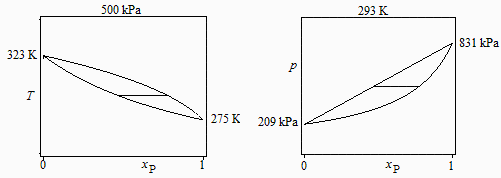
a) Diagramas esquemáticos T-x y p-x de todas las mezclas posibles a esa presión y esa temperatura, respectivamente, indicando los valores de los extremos (sustancias puras).  

Supondremos que se trata de n-butano.

>	'p1'=subs(dat,p1);Tv=T[v](pv);Tv1_:=solve(subs(dat,p1)=pv1(T),T);'Tv1_'=TKC(%);Tv2_:=solve(subs(dat,p1)=pv2(T),T);'Tv2_'=TKC(%);'T1'=subs(dat,T0);pv=p[v](T);pv1_:=evalf(subs(dat,pv1(T0)));pv2_:=evalf(subs(dat,pv2(T0)));

Los valores extremos se deducen del equilibrio líquido-vapor de cada sustancia pura (Clapeyron o Antoine).:

-para propano puro a p1=500 kPa Tv1=2 ºC, para butano puro Tv2=50 ºC;

-para propano puro a 20 ºC pv1=830 kPa y para el butano pv2=210 kPa.

Dentro habrá mezcla bifásica, pues la masa es mucha para ser todo gas a esa presión, y poca para llenarlo del todo.

El estado termodinámico parece sobredeterminado, pues la variana es V=2+C-F=2+2-2=2 y nos dan tres variables intensivas: p=500 kPa, T=20 ºC (estará atemperado con el ambiente), y rho=m/V=20/0,05=400 kg/m3. Tal vez sea que las medidas son redundantes.

b) Composición en el interior (fracciones molares de cada fase).

>	sol1_:=subs(dat,evalf(subs(p=p1,pv1=pv1(T),pv2=pv2(T),T=T0,dat,sol1)));sol2_:=subs(sol1_,dat,sol2);M0m:=x01*M1+x02*M2;M0m_:=subs(M1=M,dat1,M2=M,dat2,dat,M0m);ntot:=mtot/(M0m);ntot_:=subs(M1=M,dat1,M2=M,dat2,ntot);

i.e.  hay 392 moles en total, el 89,7% están en fase líquida (siendo el 47% de propano y el 53% de butano), y el 10,3% restante están en fase gaseosa (siendo el 78% de propano y el 22% de butano).

c) Masa de vapor.

Un límite superior sería considerar que el gas ocupa casi todo el volumen, y es casi todo del más denso (butano).

>	mgasmax:=p1*V*M2/(R[u]*T0);mgasmax_:=subs(Const,M2=M,dat2,mgasmax);

i.e. la masa de vapor será <0,6 kg. Calculándola con xv0:

>	mv:=nv/Mv;nv:='xv0*ntot';nv_:=subs(sol2_,xv0*ntot_);Mv:=xv1*M1+xv2*M2;Mv_:=subs(sol1_,M1=M,dat1,M2=M,dat2,Mv);mv_:=nv_*Mv_;

¡Vaya! No es posible; no puede tratarse de incertidumbres en las medidas (la diferencia es demasiado grande). Uno de los 3 datos sobra; relajaremos la suposición de que estaba atemperado el interior con el exterior, y determinemos la temperatura interior, que será menor porque sabemos que no hay tanto vapor. Pero antes, podemos estimar el nivel de líquido, pues al ser la masa de vapor <0,6 kg, la masa de líquido será prácticamente la total (y su composición también), con lo que podemos calcular el volumen que ocupa con el modelo de mezcla ideal, aunque al ser las densidades líquidas de las dos sustancias tan parecidas, también podría usarse un valor medio cualquiera.

>	eqVid:=Vliq/mtot=x01/rhoL1+x02/rhoL2;rhoL1:=subs(dat1,rho);rhoL2:=subs(dat2,rho);Vliq_:=solve(subs(dat,eqVid),Vliq);Vgas:=V-Vliq;Vgas_:=subs(dat,(V-Vliq_));mgas:='p1*Vgas*Mgas/(R[u]*T0)';Mgas:=xv1*M1+xv2*M2;Mgas:=M1;mgas_:=subs(Const,Vliq=Vliq_,M1=M,dat1,sol1_,sol2_,mgas);

i.e. i.e. hay 34,5 L de líquido y sólo 15,5 L de gas, y además mayoritariamente propano, por lo que la masa de la fase vapor será ligeramente superior a 0,14 kg (porque no será todo propano, pero bastante inferior al límite de 0,6 kg antes calculado), la cual hemos despreciado frente a los 20 kg totales para calcular el nivel de líquido.

Calcularemos la T1 por iteraciones (el problema es no lineal):

Si fuese T1=15 ºC en vez de 20 ºC.

>	T1_:=288.15*K_;sol1_:=subs(dat,evalf(subs(p=p1,pv1=pv1(T),pv2=pv2(T),T=T1_,dat,sol1)));sol2_:=subs(sol1_,dat,sol2);

¡Vaya! es muy sensible; a 15 ºC no hay mezcla bifásica.

Si fuese T1=19 ºC en vez de 20 ºC.

>	T1_:=292.15*K_;sol1_:=subs(dat,evalf(subs(p=p1,pv1=pv1(T),pv2=pv2(T),T=T1_,dat,sol1)));sol2_:=subs(sol1_,dat,sol2);nv:='xv0*ntot';nv_:=subs(sol2_,xv0*ntot_);Vv:='nv*R[u]*T1/p1';Vv_:=subs(Const,dat1,nv_*R[u]*T1_/p1);Mv:=xv1*M1+xv2*M2;Mv_:=subs(sol1_,M1=M,dat1,M2=M,dat2,Mv);mv_:=nv_*Mv_;

Bueno, ya nos da bifásica pero todavía no ajusta el volumen.

Si fuese T1=18,7 ºC en vez de 20 ºC ya se ajustaría todo suficientement bien.

>	T1_:=291.85*K_;sol1_:=subs(dat,evalf(subs(p=p1,pv1=pv1(T),pv2=pv2(T),T=T1_,dat,sol1)));sol2_:=subs(sol1_,dat,sol2);nv:='xv0*ntot';nv_:=subs(sol2_,xv0*ntot_);Vv:='nv*R[u]*T1/p1';Vv_:=subs(Const,dat1,nv_*R[u]*T1_/p1);Mv:=xv1*M1+xv2*M2;Mv_:=subs(sol1_,M1=M,dat1,M2=M,dat2,Mv);mv_:=nv_*Mv_;

Aunque DT=20-18,7=1,3 ºC de incertidumbre es grande, tal vez combinada con la incertidumbre en la presión cayese dentro de límites razonables.

Por ejemplo, si la temperatura interior fuese 20 ºC (i.e. atemperado) y la presión interior fuese 512 kPa en vez de los 500 kPa del enunciado, también casaría todo.

>	sol1_:=subs(dat,evalf(subs(p=518.2e3*Pa_,pv1=pv1(T),pv2=pv2(T),T=T0,dat,sol1)));sol2_:=subs(sol1_,dat,sol2);nv:='xv0*ntot';nv_:=subs(sol2_,xv0*ntot_);Vv:='nv*R[u]*T1/p1';Vv_:=subs(Const,dat1,nv_*R[u]*T1_/p1);Mv:=xv1*M1+xv2*M2;Mv_:=subs(sol1_,M1=M,dat1,M2=M,dat2,Mv);mv_:=nv_*Mv_;

Conclusión. La medida de la presión y de la temperatura no es un buen método para estimar el nivel de líquido en un recipiente con mezcla bifásica, debido a la amplificación de las incertidumbres; la medida de la masa total es mucho mejor.

>