>	restart:#"m07_p40"

Dentro de un recipiente de 10 litros hay una mezcla de propano y n-butano a 400 kPa de presión manométrica en un ambiente a 20 ºC y 100 kPa. Se pide:

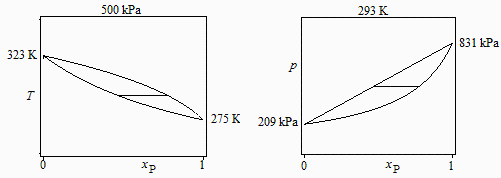
a) Diagramas esquemáticos T-x y p-x de todas las mezclas posibles a esa presión y esa temperatura, respectivamente, indicando los valores de los extremos (sustancias puras).  

b) Intervalo de composiciones de los posibles estados de equilibrio bifásico en el interior.

c) Composición interior si la proporción propano/butano fuese equiponderal.

d) Masa interior.

Datos:

>	read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):Digits:=5:

>	su1:="C3H8":su2:="C4H10":dat:=[V=0.010*m_^3,T0=(20+273.15)*K_,p1=(400+100)*1e3*Pa_,y01=1/2];

>	g1dat:=get_gas_data(su1):l1dat:=get_liq_data(su1):g2dat:=get_gas_data(su2):l2dat:=get_liq_data(su2):dat1:=op(dat),g1dat,l1dat,Const,SI2,SI1:dat2:=op(dat),g2dat,l2dat,Const,SI2,SI1:pv1:=proc(T) global su1;get_pv_data(su1);RETURN(pv(T)):end:pv2:=proc(T) global su1;get_pv_data(su2);RETURN(pv(T)):end:

>	eqNV:=xv1+xv2=1;eqNL:=xl1+xl2=1;eqC1:=xv1*xv0+xl1*xl0=x01;eqC2:=xv2*xv0+xl2*xl0=x02;eqE1:=xv1/xl1=pv1/p;eqE2:=xv2/xl2=pv2/p;sol1:=solve({eqNV,eqNL,eqE1,eqE2},{xv1,xv2,xl1,xl2});sol2:=solve({eqC1,eqC2},{xv0,xl0});

a) Diagramas esquemáticos T-x y p-x de todas las mezclas posibles a esa presión y esa temperatura, indicando los valores de los extremos (sustancias puras).

>	'p1'=subs(dat,p1);Tv=T[v](pv);Tv1_:=solve(subs(dat,p1)=pv1(T),T);'Tv1_'=TKC(%);Tv2_:=solve(subs(dat,p1)=pv2(T),T);'Tv2_'=TKC(%);'T1'=subs(dat,T0);pv=p[v](T);pv1_:=evalf(subs(dat,pv1(T0)));pv2_:=evalf(subs(dat,pv2(T0)));

Los valores extremos se deducen del equilibrio líquido-vapor de cada sustancia pura (Clapeyron o Antoine).:

-para propano puro a p1=500 kPa Tv1=2 ºC, para butano puro Tv2=50 ºC;

-para propano puro a 20 ºC pv1=830 kPa y para el butano pv2=210 kPa.

b) Intervalo de composiciones de los posibles estados de equilibrio bifásico en el interior.

Con el modelo de mezcla ideal:

>

x1boil:='(p1-pv2(T))/(pv1(T)-pv2(T))';x1dew:='(1/p1-1/pv2(T))/(1/pv1(T)-1/pv2(T))';x1boil_:=evalf(subs(T=T0,dat,x1boil));x1dew_:=evalf(subs(T=T0,dat,x1dew));y1boil_:=x1boil_*subs(dat1,M)/(x1boil_*subs(dat1,M)+(1-x1boil_)*subs(dat2,M));y1dew_:=x1dew_*subs(dat1,M)/(x1dew_*subs(dat1,M)+(1-x1dew_)*subs(dat2,M));

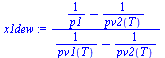i.e. si la mezcla está a 20 ºC y 500 kPa, sólo puede haber mezcla bifásica para fracciones molares de propano en el rango 0,47..0,78, correspondiente a fracciones másicas de propano en el rango 0,40..0,73 (si hubiera menos propano la mezcla sería líquida, y si hubise más sería una mezcla gaseosa).

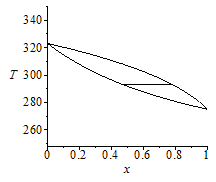
Los diagramas T-x y p-x a escala serían:

>	plot(subs(dat,SI0,{[[x1boil_,T0],[x1dew_,T0]],solve(x=x1boil,T),solve(x=x1dew,T)}),x=0..1,'T'=250..350,color=black);pboil:=x*pv1+(1-x)*pv2;pdew:=pv1/(x+(1-x)*pv1/pv2);plot(subs(pv1=pv1_,pv2=pv2_,dat,SI0,{[[x1boil_,p1],[x1dew_,p1]],pboil,pdew}),x=0..1,'p'=00..1e6,color=black);

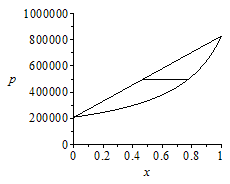c) Composición interior si la proporción propano/butano fuese equiponderal.

>	eqx01:=x01=y01/M1/(y01/M1+y02/M2);'y01'=subs(dat,y01);eqx01:=x01=subs(dat,y01/subs(dat1,M)/(y01/subs(dat1,M)+(1-y01)/subs(dat2,M)));sol1_:=subs(dat,evalf(subs(p=p1,pv1=pv1(T),pv2=pv2(T),T=T0,dat,sol1)));sol2_:=subs(sol1_,x02=1-x01,eqx01,sol2);

i.e. a 20 ºC, 500 kPa y 50% en peso de propano (57% molar), la fracción molar de líquido es del 68% (con 47% de P y 53% de B), y la de gas es del 32% (con 78% de P y 22% de B).

Nótese que los valores dentro de cada fase coinciden con los determinados en el punto anterior.

Con los datos del NIST da 71% molar de líquido (con 49% de P y 51% de B), y 29% molar de gas (con 77% de P y 23% de B).

d) Masa interior en el caso anterior

Una primera aproximación, sabiendo que la cantidad de sustancia en fase vapor no es despreciable, es suponer que ésta ocupa casi todo el volumen (pues la misma cantidad de líquido ocuparía unas mil veces menos), con lo cual podemos estimar la cantidad de sustancia en fase gaseosa.

>	nVapp:=p1*V/(R[u]*T1);nVapp_:=subs(T1=T0,Const,dat,dat1,%);eqnLapp:=xv0='nVapp/(nVapp+nLapp)';nLapp_:=nVapp_*subs(sol2_,1/xv0-1);MmL_:=subs(M1=M,g1dat,M2=M,g2dat,sol1_,xl1*M1+xl2*M2);MmV_:=subs(M1=M,g1dat,M2=M,g2dat,sol1_,xv1*M1+xv2*M2);mVapp_:=nVapp_*MmV_;mLapp_:=nLapp_*MmL_;mTapp_:=mVapp_+mLapp_;

Si lo hacemos exactamente, con las composiciones conocidas, calculamos las masas molares (MmL y MmV), las densidades (rhoL y rhoV), las masa en función del volumen líquido VL (mL y mV), las cantidades de sustancia correspondientes (nL y nV), y finalmente determinamos VL obligando a que nV/(nL+nV)=xv0.

>

eqv:=v=x1*v1+x2*v2;eqrhoL:=MmL/rhoL=xl1*M1/rho1+xl2*M2/rho2;eqrhoV:=MmV/rhoV=xv1*R[u]*T0/p1+xv2*R[u]*T0/p1;rhoL_:=subs(M1=subs(dat1,M),M2=subs(dat2,M),rho1=subs(dat1,rho),rho2=subs(dat2,rho),MmL=MmL_,sol1_,solve(eqrhoL,rhoL));rhoV_:=subs(dat1,subs(MmV=MmV_,sol1_,Const,dat,solve(eqrhoV,rhoV)));nL:=rhoL*VL/MmL;nV:=rhoV*(V-VL)/MmV;eq:='nL/(nL+nV)'=xl0;eq_:=subs(dat,rhoL_*VL/MmL_/(rhoL_*VL/MmL_+rhoV_*(V-VL)/MmV_)=subs(sol2_,xl0));VL_:=solve(%,VL);'VL_'=VL_*1e6*cm3_/m_^3;mL_:=rhoL_*VL_;mV_:=subs(dat,rhoV_*(V-VL_));mT_:=mL_+mV_;

i.e. hay 0,37 litros de líquido (y 9,63 L de gas). La masa total es de 0,31 kg (0,22 kg de L y 0,09 kg de V). Con los datos del NIST da mT=0,38 kg (rhoT=38,5 kg/m3, rhoL=545 kg/m3 y rhoV=10,9 kg/m3).

>

>

ADICIONAL

En el límite de líquido saturado, la densidad sería la de una mezcla líquida con esa composición (xP=0,47; xB=0,53), y en el límite de vapor saturado la densidad sería la de una mezcla gaseosa con esa composición (xP=0,78; xB=0,22).

>

eqrhoL:=V/(mL/MmL)=x1*M1/rho1+x2*M2/rho2;x1_:=x1boil_;x1__:=x1_:x2_:=1-x1_;MmL_:=subs(M1=M,g1dat,M2=M,g2dat,x1_*M1+x2_*M2);mL_:=subs(MmL=MmL_,M1=M,rho1=rho,g1dat,l1dat,M2=M,rho2=rho,g2dat,l2dat,x1=x1_,x2=x2_,dat,solve(eqrhoL,mL));eqrhoV:=V/(mV/MmV)=x1*R[u]*T0/p1+x2*R[u]*T0/p1;x1_:=x1dew_;x2_:=1-x1_;MmV_:=subs(M1=M,g1dat,M2=M,g2dat,x1_*M1+x2_*M2);mV_:=subs(MmV=MmV_,Const,x1=x1_,x2=x2_,dat,SI2,solve(eqrhoV,mV));

Si todo fuera líquido (xP<0,47):

>

n:=3:for i from 0 to n do x1||i:=x1__*i/n;x2_:=1-%;MmL_:=subs(M1=M,g1dat,M2=M,g2dat,x1||i*M1+x2_*M2);mL||i:=subs(MmL=MmL_,M1=M,rho1=rho,g1dat,l1dat,M2=M,rho2=rho,g2dat,l2dat,x1=x1||i,x2=x2_,dat,solve(eqrhoL,mL));print(`ì=`,i,`  x1=`,x1||i,`  mL=`,mL||i);od:pl1:=plot(subs(SI0,[seq([x1||i,mL||i],i=0..n)]),xP=0..1,mT_kg=0..6):

Si todo fuera vapor (xP>0,78):

>	n:=3:for i from 0 to n do x1||i:=x1_+(1-x1_)*i/n;x2_:=1-%;MmV_:=subs(M1=M,g1dat,M2=M,g2dat,x1||i*M1+x2_*M2);mV||i:=subs(MmV=MmV_,Const,x1=x1||i,x2=x2_,dat,SI2,solve(eqrhoV,mV));print(`ì=`,i,`  x1=`,x1||i,`  mV=`,mV||i);od:pl2:=plot(subs(SI0,[seq([x1||i,mV||i],i=0..n)]),xP=0..1):

Si hay líquido y vapor, llamando phi a la fracción molar global de vapor (phi=xv0):

>

n:=9:for i from 0 to n do x1||i:=x1__+(x1_-x1__)*(i/n)^2; x2_:=1-%;sol2_:=subs(x01=x1||i,x02=1-x1||i,dat,sol1_,sol2);MmL_:=subs(M1=M,g1dat,M2=M,g2dat,x1||i*M1+x2_*M2);rhoL_:=subs(rho1=rho,l1dat,rho2=rho,l2dat,x1||i*rho1+x2_*rho2);phi||i:=subs(sol2_,MmL=MmL_,rhoL=rhoL_,Const,dat,SI2,1/(p1*xl0*MmL/(R[u]*T0*xv0*rhoL)+1));mL:=subs(dat,rhoL_*(1-phi||i)*V);mV:=subs(Const,dat,SI2,phi||i*V*p1*MmV_/(R[u]*T0));m||i:=mL+mV;print(`ì=`,i,`  x1=`,x1||i,`  phi=`,phi||i,`  mT=`,m||i); od:pl3:=plot(subs(SI0,[seq([x1||i,m||i],i=0..n)]),xP=0..1):pl4:=plot(subs(SI0,[[x1__,0],[x1__,mL_],[x1_,mV_],[x1_,0]]),xP=0..1,linestyle=dash):with(plots):display([pl1,pl2,pl3,pl4]);

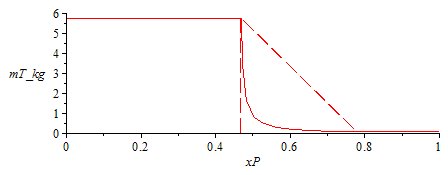Obsérvese qué deprisa cae el masa interior con la fracción molar global (se ha dibujado a trazos la interpolación lineal). La explicación es que, como la diferencia de densidades entre la fase líquida y la vapor es tan grande, a poco que se incremente el porcentaje en masa o molar de vapor, esto requiere volúmenes de vapor muy grandes.

>