>	restart;#"m07_p30"

A una cámara de expansión de 1 m3 entra una corriente equimolar de n-butano y propano a 20 ºC, en estado líquido, saliendo en régimen estacionario por una tubería el vapor formado y por otra el líquido residual. Sabiendo que la expansión es hasta 95 kPa, se pide:
a) (Opcional; sustancia pura) Considerar que se trata de propano (o n-butano) puro. Hacer un esquema de la instalación, indicar las ecuaciones relevantes, determinar la presión mínima de alimentación y la temperatura de salida, representar la entalpía de esa sustancia en función de la temperatura, determinar la cantidad de líquido en el depósito y la relación de gastos de salida respecto a la entrada.
b) Hacer un esquema de la instalación y determinar la presión mínima de alimentación.
c) Representar la entalpía de la mezcla en función de la temperatura de salida y calcular ésta.
d) Cantidad de líquido en el depósito.
e) Composiciones y gastos de salida.

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc): su1:="C3H8":su2:="C4H10":dat:=[V=1*m_^3,x1=0.5,T1=(20+273)*K_,p2=95e3*Pa_];

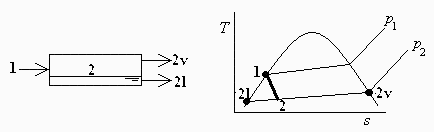
Esquema:

Sistema:=[mezcla en el volumen de control V]

Estados:=[1=entrada,2v=salida_vap,2l=salida_liq]

Ecuaciones:

>	g1dat:=get_gas_data(su1):l1dat:=get_liq_data(su1):g2dat:=get_gas_data(su2):l2dat:=get_liq_data(su2):dat:=op(dat),Const,SI2,SI1:dat1:=g1dat,l1dat:dat2:=g2dat,l2dat:pv1:=proc(T) global su1;get_pv_data(su1);RETURN(pv(T)):end:pv2:=proc(T) global su1;get_pv_data(su2);RETURN(pv(T)):end:

>	eqNV:=xv1+xv2=1;eqNL:=xl1+xl2=1;eqC1:=xv1*xv0+xl1*xl0=x01;eqC2:=xv2*xv0+xl2*xl0=x02;eqE1:=xv1/xl1=pv1/p;eqE2:=xv2/xl2=pv2/p;sol1:=solve({eqNV,eqNL,eqE1,eqE2},{xv1,xv2,xl1,xl2});sol2:=solve({eqC1,eqC2},{xv0,xl0});#assign(sol1):

a) SUSTANCIA PURA. Hacer un esquema de la instalación, indicar las ecuaciones relevantes.

El balance másico lo sustituiremos por 1=xv+(1-xv).

El balance mecánico no lo consideramos: se supone fijo a una bancada.

El balance energético es el crucial: h1=h2(T)=(1-xv)*h2l+xv*h2v. De la 1ª obtengo la Tsalida y de la 2ª la xv.

El balance exergético (o el entrópico) mostraría la disipación en el interior, que siempre será positiva porque hay que alimentar a presión.

>	eqBE1:=h1=h2;eqBE2:=(1-xv)*h2l+xv*h2v;

PURA. Determinar la presión mínima de alimentación.

La presión mínima será la de vaporización a esa temperatura para esa sustancia:

>	T1=subs(dat,T1);pv1=p[v](T1);pv1_:=subs(dat,evalf(subs(dat,pv1(T1)))):'pv1'=evalf(%,3);

PURA. Determinar la temperatura de salida.

>	T2=Tv(p2);p2=subs(dat,p2);T2_:=subs(dat,evalf(subs(dat,solve(p2=pv1(T),T)))):'T2'=evalf(%,3);

PURA. Representar la entalpía de esa sustancia en función de la temperatura.

Modelo de sustancia perfecta. Ref.: líquido en el punto triple (href=sref=0). Introducimos una pequeña anchura artificial de cambio de fase, eps, para hacer monótona la función h(T).

NOTA: trabajaremos con valores másicos, i.e., x=fracciones másicas, h=H/m.

>

hliq:=c[L]*(T2-Tref);hliq:=subs(dat1,hl(T));hvap:=c[L]*(Tb-Tref)+hlvb+c[p]*(T2-Tb);hvap:=subs(dat1,hv(T));h1_:=subs(T=T1,dat,hliq):'h1'=evalf(%,2);h2l_:=subs(T=T2_,hliq):'h2l'=evalf(%,2);h2v_:=subs(T=T2_,hvap):'h2v'=evalf(%,2);eps:=1e-3*K_;h2(T):=piecewise(T<T2_,hliq,T>T2_+eps,hvap,h2l_+(h2v_-h2l_)*(T-T2_)/eps);plot(subs(SI0,{[[0,h1_],[1000,h1_]],h2(T)}),T=200..300);solve(subs(SI0,h1_=h2(T)),T)*K_:'T2'=evalf(%,3);

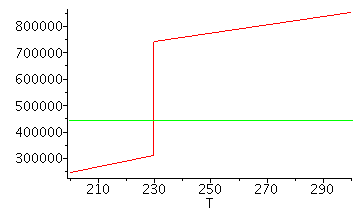PURA. Determinar la cantidad de líquido en el depósito y la relación de gastos de salida respecto a la entrada.

>	x2=(h1-h2l)/(h2v-h2l);x2_:=(h1_-h2l_)/(h2v_-h2l_):'x2'=evalf(%,2);eqVol_Bif:='V/m[tot]=(1-x2)/rho+x2*R*T/p';mtot_:=subs(dat,dat1,dat,V/((1-x2_)/rho+x2_*R*T2_/p2)):'m[tot]'=evalf(%,2);mv_:=mtot_*x2_:'m[vap]'=evalf(%,2);ml_:=mtot_-mv_:'m[liq]'=evalf(%,2);VL_:=subs(dat1,ml_/rho):'V[liq]'=evalf(%,2);

i.e., si entrase propano puro, la presión de alimentación habría de ser >=828 kPa, la temperatura de salida sería de 231 K, la cantidad de líquido en el depósito sería de 8,2 L, 4,8 kg (y 2,2 kg de vapor), y los gastos de salida serían del 31% en peso por la salida de arriba (vapores) y del 67% por la salida de abajo (líquido).

PURA, pero n-butano. (Basta cambiar su1 por su2.)

Si entrase n-butano puro, la presión de alimentación habría de ser >=208 kPa, la temperatura de salida sería de 270 K, la cantidad de líquido en el depósito sería de 25 L, 14 kg (y 2,4 kg de vapor), y los gastos de salida serían del 14% en peso por la salida de arriba (vapores) y del 86% por la salida de abajo (líquido).

MEZCLA. NOTA: ahora usaremos variables molares, i.e., x=fracciones molares, h=H/n..

b) Hacer un esquema de la instalación y determinar la presión mínima de alimentación.

La presión mínima será la de vaporización a esa temperatura y con esa composición de líquido. pvap=Sum(xvap,i*p)=Sum(xliq,i*pvi).

>	T1=subs(dat,T1);pboil:=x[L1]*pv1+x[L2]*pv2;pv1_:=subs(dat,evalf(subs(dat,pv1(T1)))):'pv1'=evalf(%,3);pv2_:=subs(dat,evalf(subs(dat,pv2(T1)))):'pv2'=evalf(%,3);pboil_:=subs(dat,x1*pv1_+(1-x1)*pv2_):'pboil'=evalf(%,3);

i.e. si entrase una mezcla equimolar, la presión de alimentación habría de ser >=518 kPa para que estuviese líquido.

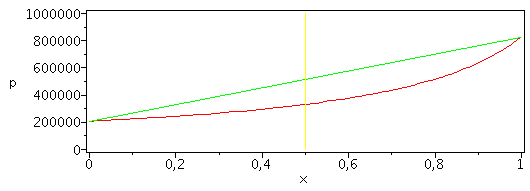
Gráfico de la presión de vaporización (pboil) y de la presión de condensación (pdew) para cualquier concentración:

>	pboil:='x*pv1_+(1-x)*pv2_';pdew:='pv1_/(x+(1-x)*pv1_/pv2_)';plot(subs(SI0,{[[0.5,0],[0.5,1e6]],pboil,pdew}),x=0..1,'p'=00..1e6);

c) Representar la entalpía de la mezcla en función de la temperatura de salida y calcular ésta.

Una buena aproximación es suponer que la h(T) varía linealmente con T en la región bifásica:

>

h2(T):=piecewise(T<Tboil,'hliq',T>Tdew,'hvap',h2l+(h2v-h2l)*(T-Tboil)/(Tdew-Tboil));p2_:=subs(dat,p2);T=Tv(p2,su);T1_:=solve(subs(dat,p2)=pv1(T),T):'T1'=evalf(%,3);T2_:=solve(subs(dat,p2)=pv2(T),T):'T2'=evalf(%,3);eqTboil:=subs(sol1,p=p2,x1=xl1);Tboil_:=fsolve(subs(sol1,p=p2,pv1=pv1(T),pv2=pv2(T),dat,SI0,x1=xl1),T=100..500)*K_:'T[boil]'=evalf(%,3);eqTdew:=subs(sol1,p=p2,x1=xv1);Tdew_:=fsolve(subs(sol1,p=p2,pv1=pv1(T),pv2=pv2(T),dat,SI0,x1=xv1),T=100..500)*K_:'T[dew]'=evalf(%,3);hliq:=xl1*hl1+xl2*hl2;hl=hl(T);hl1_:=subs(dat1,M*hl(T)):hl2_:=subs(dat2,M*hl(T)):hliq_:=expand(subs(dat,x1*hl1_+(1-x1)*hl2_)):'hliq'=evalf(%,2);hvap:=xv1*hv1+xv2*hv2;hv=hv(T);hv1_:=expand(subs(dat1,SI2,M*hv(T))):hv2_:=subs(dat2,M*hv(T)):hvap_:=expand(subs(dat,SI2,x1*hv1_+(1-x1)*hv2_)):'hvap'=evalf(%,2);;h2l_:=subs(T=Tboil_,hliq_):'h2l'=evalf(%,2);h2v_:=subs(T=Tdew_,hvap_):'h2v'=evalf(%,2);h2(T):=piecewise(T<Tboil_,hliq_,T>Tdew_,hvap_,h2l_+(h2v_-h2l_)*(T-Tboil_)/(Tdew_-Tboil_)):'h2(T)'=evalf(%,3);h1_:=subs(T=T1,dat,hliq_):'h1'=evalf(%,2);plot(subs(SI0,{[[0,h1_],[1000,h1_]],h2(T)}),T=200..300);solve(subs(SI0,h1_=h2(T)),T)*K_:'T2'=evalf(%,3);

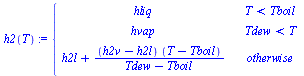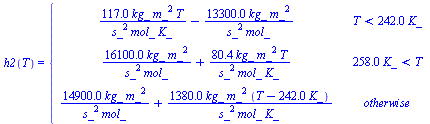La solución exacta sería en función de la cantidad de líquido xliq0 y las concentraciones xliq1 y xvap1.

>

hbif:=xl0*(xl1*hl1+xl2*hl2)+xv0*(xv1*hv1+xv2*hv2);sol1;sol2;hbif_:=subs(sol2,sol1,hl1=subs(dat1,M*hl(T)),hl2=subs(dat2,M*hl(T)),hv1=subs(dat1,M*hv(T)),hv2=subs(dat2,M*hv(T)),x01=x1,x02=1-x1,p=p2,pv1=pv1(T),pv2=pv2(T),dat,hbif):plot(subs(SI0,[hbif_,h2l_+(h2v_-h2l_)*(T-Tboil_)/(Tdew_-Tboil_)]),T=subs(SI0,Tboil_)..subs(SI0,Tdew_),subs(SI0,h2l_)..subs(SI0,h2v_));h2(T):=piecewise(T<Tboil_,hliq,T>Tdew_,hvap,hbif_):T2__:=fsolve(subs(SI0,h1_=hbif_),T=200..300)*K_:'T2'=evalf(%,3);

i.e., la temperatura de salida es T2=246 K.

Se ha dibujado la h(T) en la región bifásica con ambos modelos (lineal y exacto). La aproximación lineal es siempre buena, pero aquí es perfecta.

d) Cantidad de líquido en el depósito.

La cantidad de líquido es xliq0. Es muy ilustrativo dibujar (aunque sea esquemáticamente) el diagrama T-x a la p2 de salida.

>

T2_:=T2__:sol1;sol1_:=subs(p=p2,pv1=pv1(T2_),pv2=pv2(T2_),dat,sol1):evalf(%,2);sol2;sol2_:=subs(sol1_,x01=x1,x02=1-x1,dat,sol2):evalf(%,2);p2_:=subs(dat,p2);T1_:=solve(subs(dat,p2)=pv1(T),T):'T1'=evalf(%,3);T2_:=solve(subs(dat,p2)=pv2(T),T):'T2'=evalf(%,3);xboil:='(p2_-pv2(T))/(pv1(T)-pv2(T))';xdew:='(1/p2_-1/pv2(T))/(1/pv1(T)-1/pv2(T))';plot(subs(dat,SI0,{[[x1,0],[x1,1000]],[[0,T2__],[1,T2__]],solve(x=xboil,T),solve(x=xdew,T)}),x=0..1,'T'=200..300,color=black);

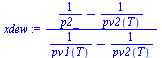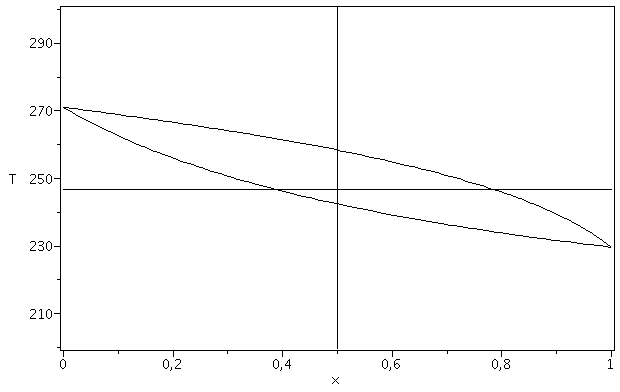i.e., del total de moles en el depósito (50% propano y 50% butano), 72% están en fase líquida y 28% gaseosa. De los de la fase líquida, 39% son de propano y 61% de butano, mientras que de los de la fase vapor 79% son de propano y 21% de butano. Evidentemente, el componente más volátil está más vaporizado.

e) Composiciones y gastos de salida.

En régimen estacionario ha de salir un 72% del gasto molar de entrada por la tubería de líquido, y un 28% por la de gas.

Pasando a valores másicos:

>

y[i]:=x[i]*M[i]/Sum(x[i]*M[i],i=1..C);y1:=x1*M1/(x1*M1+x2*M2);y1_:=subs(x2=1-x1,dat,M1=M,dat1,M2=M,dat2,y1):'y1'=evalf(%,2);yv1:=xv1*M1/(xv1*M1+xv2*M2);yv1_:=subs(sol1_,dat,M1=M,dat1,M2=M,dat2,yv1):'yv1'=evalf(%,2);yl1:=xl1*M1/(xl1*M1+xl2*M2);yl1_:=subs(sol1_,dat,M1=M,dat1,M2=M,dat2,yl1):'yl1'=evalf(%,2);yv1:='yv1':yl1:='yl1':eqC1_:=y01=yv0*yv1+yl0*yl1;eqC2_:=y02=yv0*yv2+yl0*yl2;sol3:=solve({eqC1_,eqC2_},{yv0,yl0});sol3_:=subs(y01=y1_,y02=1-y1_,yv1=yv1_,yv2=1-yv1_,yl1=yl1_,yl2=1-yl1_,dat,M1=M,dat1,M2=M,dat2,sol1_,sol3):evalf(%,2);

i.e., equimolar (50% propano y 50% butano) implica 43% de propano y 57% de butano globalmente (entrada, interior, y salida). En el interior, 74% de la masa total está en fase líquida y 26% gaseosa. De los de la fase líquida, 33% son de propano y 67% de butano, mientras que de los de la fase vapor 74% son de propano y 26% de butano. Evidentemente, el componente más volátil está más vaporizado.

¿Y si cerrásemos un de los conductos de salida? Pues saldría la mezcla bifásica por la otra.

¿Y si cerrásemos el otro también? Pues que no puede entrar.

¿Y si no lo cerramos del todo? Pues que aumentará la presión en el interior de la cámara, y también el nivel de líquido. Si se llegara a los 828 kPa sería todo líquido. A la salida habría que volver a resolver el problema de despresurización isoentálpica.

>

eqrhoV:=rho=p2*Mm/(R[u]*T2);eqMm:=Mm=xv1*M1+xv2*M2;eqMm_:=subs(sol1_,M1=M,dat1,M2=M,dat2,eqMm):evalf(%,2);eqrhoV_:=subs(T2=T2_,eqMm_,dat,eqrhoV):'eqrhoV'=evalf(%,3);eqrhoL:=rho=1/Sum('y[i]'/rho[i],i=1..C);eqrhoL:=rho=1/(yl1/rho1+yl2/rho2);eqrhoL_:=rho=subs(yl1=yl1_,yl2=1-yl1_,rho1=rho,dat1,rho2=rho,dat2,rhs(eqrhoL)):'eqrhoL'=evalf(%,3);eqV:=V/mtot=(1-yv0)/rho[L,mix]+yv0/rho[V,mix];mtot_:=subs(sol3_,dat,V/(yl0/subs(eqrhoL_,rho)+yv0/subs(eqrhoV_,rho))):'mtot'=evalf(%,2);mvap:=yv0*mtot;mvap_:=subs(sol3_,mtot=mtot_,mvap):'mvap'=evalf(%,2);mliq_:=mtot_-mvap_:'mliq'=evalf(%,2);Vliq:='mliq/rhoL';Vliq_:=subs(eqrhoL_,mliq_/rho):'Vliq'=evalf(%,2);

i.e., dentro de V hay 7,6 kg de mezcla bifásica, 2 kg de mezcla vapor y 5,6 kg de mezcla líquida.

Nótese que estos valores están en medio de los extremos inicialmente calculados para las sustancias puras; e.g. para propano puro habría 8 L de líquido, para butano puro 25 L, y para la mezcla equimolar 9,8 L.

>