>	restart:#"m07_p26"

Un modelo muy simplificado de una torre de enfriamiento evaporativo consiste en un cajn con agua, en rgimen casi-estacionario, donde el agua recibe una potencia trmica  =100 kW que se compensa con la evaporacin de una cantidad de agua  , segn se esquematiza en la figura (supngase que el agua del cajn apenas se calienta porque realmente la evaporacin se intensifica mucho en la práctica rociando esa misma agua desde una cierta altura para que el contacto con el aire ambiente sea mucho más efectivo). Inicialmente hay en el cajn 300 litros de agua del grifo con una concentracin de 0,5 g/kg de sales. Se pide:
a) Balances másicos y energtico para el volumen de control ocupado por el agua lquida.
b) Gasto de vapor producido.
c) Sabiendo que cuando se gasta la mitad del agua se vuelve a rellenar rápidamente con agua del grifo, determinar el periodo entre 'rellenadas'.
d) Sabiendo que cuando se alcanza una concentracin salina de 10 g/kg se tira toda el agua rápidamente y se vuelve a rellenar con agua del grifo, determinar el periodo entre purgas.
e) Representar esquemáticamente la variacin con el tiempo de la concentracin salina.

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):

>	su1:="H2O":dat:=[Qdot=100e3*W_,V1=0.3*m_^3,y1=0.5e-3,V2=0.15*m_^3,y3=0.01];

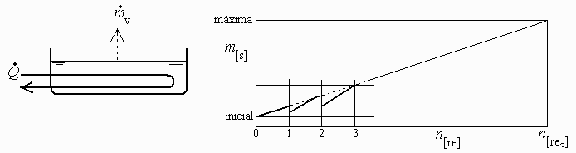
Esquema:

>

>

Eqs. const.:

>	ldat:=get_liq_data(su1):dat:=op(dat),ldat,Const,SI2,SI1:get_pv_data(su1):

a) Balances másicos y energtico para el volumen de control ocupado por el agua lquida.

>	eqBMw:=Diff(m[w],t)=-mdot[v];eqBMs:=Diff(y[s]*m[w],t)=0;eqBE:=Diff(m[w]*c*(T-T[ref]),t)=Qdot-mdot[v]*h[v];

b) Gasto de vapor producido.

>	eqBE:=-mdot[v]*c*(T-T[ref])=Qdot-mdot[v]*h[v];eqBE:=mdot[v]=Qdot/h[lv];eqBE_:=subs(h[lv]=h[lv0],dat,eqBE);

c)  Sabiendo que cuando se gasta la mitad del agua se vuelve a rellenar rpidamente con agua del grifo, determinar el periodo entre 'rellenadas'.

>	eq1:=t[re]=rho*(V1-V2)/mdot[v];eq1_:=subs(eqBE_,dat,eq1);

d) Sabiendo que cuando se alcanza una concentracin salina de 10 g/kg se tira toda el agua rpidamente y se vuelve a rellenar con agua del grifo, determinar el periodo entre purgas.

Sea n[re3] el nmero de rellenadas hasta que hay que purgar.

>	eq2:=t[pu]=t[re]*n[re3];eqBMs:=m[s3]=m[s1]+Dm[s2]*n[re3];m[s3]:=rho*V1*y3;m[s1]:=rho*V1*y1;Dm[s2]:=rho*(V1-V2)*y1;eqBMs_:=subs(dat,eqBMs);eqBMs_:=n[re3]=solve(eqBMs_,n[re3]);eq2_:=subs(eqBMs_,eq1_,eq2);'t[pu]'=evalf(rhs(%)/(3600*s_/h_),2);

e) Representar esquemticamente la variacin con el tiempo de la concentracin salina.

(ver gráfico más arriba).

En resumen, habra que rellenar cada hora y vaciar cada da y medio. Como estos valores son cortos para una operacin normal, convendrá aumentar el volumen de agua del cajn y automatizar los aportes, e incluso las purgas.

>